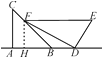
【题目】小明是一位善于思考的学生，在一次数学活动课上，他将一副直角三角板如图位置摆放，A、B、D在同一直线上，EF∥AD，∠A＝∠EDF＝90°，∠C＝45°，∠E＝60°，量得DE＝8，试求BD的长．

参考答案：

【答案】12-4

【解析】

过点F作FM⊥AD于M,利用在直角三角形中,30°角所对的直角边等于斜边的一半和平行线的性质以及等腰直角三角形的性质即可求出BD的长．

解:如图,过点F作FH⊥AB于点H.

在Rt△DEF中,∠EDF＝90°,∠E＝60°,DE＝8,

∴DF＝DE·tan∠E＝8·tan60°＝8

∵EF∥AD,

∴∠FDH＝∠DFE＝30°,

在Rt△FDH中,FH＝DF＝4,HD＝4·＝12.

又∵∠CAB＝90°,∠C＝45°,

∴HB＝FH＝4,

∴BD=HD－HB＝12－4.

关闭