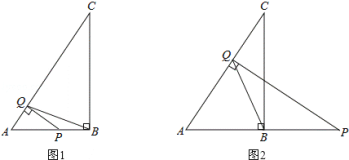
【题目】已知在△ABC中,∠ABC=90°,AB=9,BC=12.点Q是线段AC上的一个动点,过点Q作AC的垂线交射线AB于点P.当△PQB为等腰三角形时,则AP的长为_______.
【答案】5或18
【解析】
当△PQB为等腰三角形时,有两种情况: ①当点P在线段AB上时,如题图1所示.由△AQP∽△ABC即可计算AP的长;②当点P在线段AB的延长线上时,如题图2所示,利用角之间的关系,证明点B为线段AP的中点,从而可以求出AP.
∵∠A+∠APQ=90°,∠A+∠C=90°,
∴∠APQ=∠C.
∵∠A=∠A,
∴△APQ∽△ACB.
在Rt△ABC中,AB=9,BC=12,由勾股定理得:AC=15,
①当点P在线段AB上时,如题图1所示,
∵∠BPQ为钝角,
∴当△PQB为等腰三角形时,只可能是PB=PQ.
∵△APQ∽△ACB,
∴![]() ,即
,即![]() ,解得:PB=4,
,解得:PB=4,
∴AP=AB﹣PB=9-4=5;
②当点P在线段AB的延长线上时,如题图2所示,
∵∠QBP为钝角,
∴当△PQB为等腰三角形时,只可能是BP=BQ,
∴∠BQP=∠P,
∵∠BQP+∠AQB=90°,∠A+∠P=90°,
∴∠AQB=∠A,
∴BQ=AB,
∴AB=BP,点B为线段AB中点,
∴AP=2AB=2×9=18.
综上所述,当△PQB为等腰三角形时,AP的长为5或18.
故答案是:5或18.