【题目】在平面直角坐标系中,我们定义直线y=ax﹣a为抛物线![]() (a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
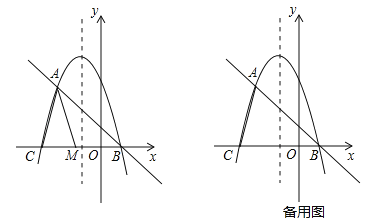
已知抛物线![]() 与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(﹣2,
;(﹣2, ![]() );(1,0);(2)N点坐标为(0,
);(1,0);(2)N点坐标为(0, ![]() ﹣3)或(
﹣3)或(![]() ,
, ![]() );(3)E(﹣1,﹣
);(3)E(﹣1,﹣![]() )、F(0,
)、F(0, ![]() )或E(﹣1,﹣
)或E(﹣1,﹣![]() )、F(﹣4,
)、F(﹣4, ![]() ).
).
【解析】试题分析:(1)由梦想直线的定义可求得其解析式,联立梦想直线与抛物线解析式可求得A、B的坐标;
(2)当N点在y轴上时,过A作AD⊥y轴于点D,则可知AN=AC,结合A点坐标,则可求得ON的长,可求得N点坐标;当M点在y轴上即M点在原点时,过N作NP⊥x轴于点P,由条件可求得∠NMP=60°,在Rt△NMP中,可求得MP和NP的长,则可求得N点坐标;
(3)当AC为平行四边形的一边时,过F作对称轴的垂线FH,过A作AK⊥x轴于点K,可证△EFH≌△ACK,可求得DF的长,则可求得F点的横坐标,从而可求得F点坐标,由HE的长可求得E点坐标;当AC为平行四边形的对角线时,设E(﹣1,t),由A、C的坐标可表示出AC中点,从而可表示出F点的坐标,代入直线AB的解析式可求得t的值,可求得E、F的坐标.
(1)∵抛物线![]() ,∴其梦想直线的解析式为
,∴其梦想直线的解析式为![]() ,联立梦想直线与抛物线解析式可得:
,联立梦想直线与抛物线解析式可得: 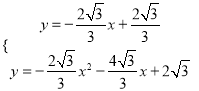 ,解得:
,解得:  或
或![]() ,∴A(﹣2,
,∴A(﹣2, ![]() ),B(1,0),故答案为:
),B(1,0),故答案为: ![]() ;(﹣2,
;(﹣2, ![]() );(1,0);
);(1,0);
(2)当点N在y轴上时,△AMN为梦想三角形,如图1,过A作AD⊥y轴于点D,则AD=2,在![]() 中,令y=0可求得x=﹣3或x=1,∴C(﹣3,0),且A(﹣2,
中,令y=0可求得x=﹣3或x=1,∴C(﹣3,0),且A(﹣2, ![]() ),∴AC=
),∴AC=![]() =
=![]() ,由翻折的性质可知AN=AC=
,由翻折的性质可知AN=AC=![]() ,在Rt△AND中,由勾股定理可得DN=
,在Rt△AND中,由勾股定理可得DN=![]() =
=![]() =3,∵OD=
=3,∵OD=![]() ,∴ON=
,∴ON=![]() ﹣3或ON=
﹣3或ON=![]() +3,当ON=
+3,当ON=![]() +3时,则MN>OD>CM,与MN=CM矛盾,不合题意,∴N点坐标为(0,
+3时,则MN>OD>CM,与MN=CM矛盾,不合题意,∴N点坐标为(0, ![]() ﹣3);
﹣3);
当M点在y轴上时,则M与O重合,过N作NP⊥x轴于点P,如图2,在Rt△AMD中,AD=2,OD=![]() ,∴tan∠DAM=
,∴tan∠DAM=![]() =
=![]() ,∴∠DAM=60°,∵AD∥x轴,∴∠AMC=∠DAO=60°,又由折叠可知∠NMA=∠AMC=60°,∴∠NMP=60°,且MN=CM=3,∴MP=
,∴∠DAM=60°,∵AD∥x轴,∴∠AMC=∠DAO=60°,又由折叠可知∠NMA=∠AMC=60°,∴∠NMP=60°,且MN=CM=3,∴MP=![]() MN=
MN=![]() ,NP=
,NP=![]() MN=
MN=![]() ,∴此时N点坐标为(
,∴此时N点坐标为(![]() ,
, ![]() );
);
综上可知N点坐标为(0, ![]() ﹣3)或(
﹣3)或(![]() ,
, ![]() );
);
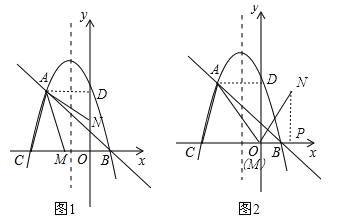

(3)①当AC为平行四边形的边时,如图3,过F作对称轴的垂线FH,过A作AK⊥x轴于点K,则有AC∥EF且AC=EF,∴∠ACK=∠EFH,在△ACK和△EFH中,∵∠ACK=∠EFH,∠AKC=∠EHF,AC=EF,∴△ACK≌△EFH(AAS),∴FH=CK=1,HE=AK=![]() ,∵抛物线对称轴为x=﹣1,∴F点的横坐标为0或﹣2,∵点F在直线AB上,∴当F点横坐标为0时,则F(0,
,∵抛物线对称轴为x=﹣1,∴F点的横坐标为0或﹣2,∵点F在直线AB上,∴当F点横坐标为0时,则F(0, ![]() ),此时点E在直线AB下方,∴E到y轴的距离为EH﹣OF=
),此时点E在直线AB下方,∴E到y轴的距离为EH﹣OF=![]() ﹣
﹣![]() =
=![]() ,即E点纵坐标为﹣
,即E点纵坐标为﹣![]() ,∴E(﹣1,﹣
,∴E(﹣1,﹣![]() );
);
当F点的横坐标为﹣2时,则F与A重合,不合题意,舍去;
②当AC为平行四边形的对角线时,∵C(﹣3,0),且A(﹣2, ![]() ),∴线段AC的中点坐标为(﹣2.5,
),∴线段AC的中点坐标为(﹣2.5, ![]() ),设E(﹣1,t),F(x,y),则x﹣1=2×(﹣2.5),y+t=
),设E(﹣1,t),F(x,y),则x﹣1=2×(﹣2.5),y+t=![]() ,∴x=﹣4,y=
,∴x=﹣4,y=![]() ﹣t,代入直线AB解析式可得
﹣t,代入直线AB解析式可得![]() ﹣t=﹣
﹣t=﹣![]() ×(﹣4)+
×(﹣4)+![]() ,解得t=﹣
,解得t=﹣![]() ,∴E(﹣1,﹣
,∴E(﹣1,﹣![]() ),F(﹣4,
),F(﹣4, ![]() );
);
综上可知存在满足条件的点F,此时E(﹣1,﹣ ![]() )、F(0,
)、F(0, ![]() )或E(﹣1,﹣
)或E(﹣1,﹣![]() )、F(﹣4,
)、F(﹣4, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
①AM=AD+MC;②AM=DE+BM;③DE2=ADCM;④点N为△ABM的外心.其中正确的个数为( )
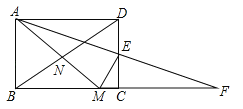
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个棱柱中,一共有八个面,则这个棱柱棱的条数有( )
A.18条B.15条C.12条D.21条
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发
 h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).
h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a﹣3b=2,那么2a﹣6b的值是( )
A.4B.﹣4C.1D.﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)参加初赛的选手共有 名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
相关试题

