搜索
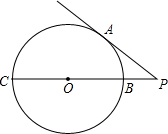
如图，PA切⊙O于A，割线PBC经过圆心O，交⊙O于B、C两点，若PA=4，PB=2，则tan∠P的值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
分析：根据PA，PB分别是⊙O的切线和割线求得OB=3；连接OA，构造直角三角形，利用三角函数的定义求解即可．
解答：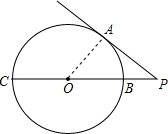
解：∵PA，PB分别是⊙O的切线和割线，
∴PA2=PB•PC．
∵PA=4，PB=2，
∴PC=8，BC=6，
∴OB=3．
连接OA，则∠OAP=90°，
tan∠P=
=
．
故选B．
解：∵PA，PB分别是⊙O的切线和割线，∴PA2=PB•PC．
∵PA=4，PB=2，
∴PC=8，BC=6，
∴OB=3．
连接OA，则∠OAP=90°，
tan∠P=
| OA |
| PA |
| 3 |
| 4 |
故选B．
点评：此题主要考查了切线的性质，勾股定理及锐角三角函数的定义等知识点的综合运用．
