【题目】在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.
(1)求证:△EMO≌△OND;
(2)若AB=AC,且∠BAC=40°,当∠DAB等于多少时,四边形ADOE是菱形,并证明.

参考答案:
【答案】(1)证明见解析(2)当∠DAB等于35°时,四边形ADOE是菱形
【解析】试题分析:(1)根据直角三角形斜边中线等于斜边一半得:DN=![]() AB,由中位线定理得:OM=
AB,由中位线定理得:OM=![]() AB,则OM=DN,同理得:ON=ME,再根据外角定理和已知证明其夹角相等,则两三角形全等;
AB,则OM=DN,同理得:ON=ME,再根据外角定理和已知证明其夹角相等,则两三角形全等;
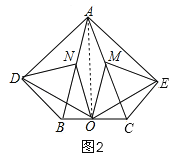
(2)连接AO,当∠DAB等于35°时,四边形ADOE是菱形,如图2,设∠DAB=x°,则∠BND=2x°,易证得OD=OE,AD=AE,因此只要AD=OD,四边形ADOE就是菱形;即∠DAO=∠AOD,列关于x的方程解出即可.
试题解析:证明:(1)∵∠ADB=90°,N是AB的中点,∴DN=![]() AB=AN,∴∠ADN=∠BAD,∵O是AB的中点,M是AC的中点,∴OM是△ABC的中位线,∴OM=
AB=AN,∴∠ADN=∠BAD,∵O是AB的中点,M是AC的中点,∴OM是△ABC的中位线,∴OM=![]() AB,OM∥AB,∴∠OMC=∠BAC,同理得:∠BNO=∠BAC,∴∠BNO=∠OMC,∵DN=
AB,OM∥AB,∴∠OMC=∠BAC,同理得:∠BNO=∠BAC,∴∠BNO=∠OMC,∵DN=![]() AB,OM=
AB,OM=![]() AB,∴DN=OM,同理得:ME=ON,∵∠BND=∠ADN+∠BAD,∠CME=∠CAE+∠AEM,∴∠BND=2∠BAD,∠CME=2∠CAE,∵∠BAD=∠CAE,∴∠BND=∠CME,∴∠BND+∠BNO=∠CME+∠OMC,即∠DNO=∠EMO,∴△EMO≌△OND;
AB,∴DN=OM,同理得:ME=ON,∵∠BND=∠ADN+∠BAD,∠CME=∠CAE+∠AEM,∴∠BND=2∠BAD,∠CME=2∠CAE,∵∠BAD=∠CAE,∴∠BND=∠CME,∴∠BND+∠BNO=∠CME+∠OMC,即∠DNO=∠EMO,∴△EMO≌△OND;
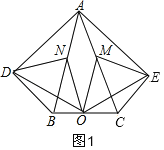
(2)当∠DAB等于35°时,四边形ADOE是菱形,理由是:
如图2,连接AO,设∠DAB=x°,则∠BND=2x°,∵AB=AC,O是BC的中点,∴AO平分∠BAC,AO⊥BC,∵∠BAC=40°,∴∠BAO=20°,在Rt△ABO中,N是AB的中点,∴ON=![]() AB=AN,∴∠BAO=∠AON=20°,∴∠BNO=40°,由(1)得:ON=
AB=AN,∴∠BAO=∠AON=20°,∴∠BNO=40°,由(1)得:ON=![]() AC,DN=
AC,DN=![]() AB,∴ON=DN,∴∠NDO=∠NOD=
AB,∴ON=DN,∴∠NDO=∠NOD=![]() (180°-∠DNO)=90°﹣
(180°-∠DNO)=90°﹣![]() (2x°+40°)=70°﹣x°,∵∠ADB=∠AEC=90°,∠BAD=∠CAE,AB=AC,∴△ADB≌△AEC,∴AD=AE,由(1)得:△EMO≌△OND,∴OD=OE,∴当AD=OD时,四边形ADOE是菱形,即∠DAO=∠AOD,x+20=70﹣x+20,x=35,∴当∠DAB等于35°时,四边形ADOE是菱形.
(2x°+40°)=70°﹣x°,∵∠ADB=∠AEC=90°,∠BAD=∠CAE,AB=AC,∴△ADB≌△AEC,∴AD=AE,由(1)得:△EMO≌△OND,∴OD=OE,∴当AD=OD时,四边形ADOE是菱形,即∠DAO=∠AOD,x+20=70﹣x+20,x=35,∴当∠DAB等于35°时,四边形ADOE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用 来表示
来表示 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为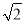 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2< <3,∴
<3,∴ 的整数部分为2,小数部分为
的整数部分为2,小数部分为 ﹣2.
﹣2.请解答:
(1)
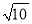 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .(2)如果
 的小数部分为a,
的小数部分为a,  的整数部分为b,求a+b-
的整数部分为b,求a+b- 的值;
的值;(3)已知:x是3+
 的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a﹣a=2B.5x﹣3x=2x
C.y2﹣y=yD.3a2+2a2=5a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】比1小2的数是( )
A.﹣1B.﹣2C.﹣3D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】若A=(x+y)2,B=(x﹣y)2,则A﹣B=_____.
相关试题

