【题目】如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;② ![]() =
= ![]() ;③S△PDQ=
;③S△PDQ= ![]() ;④cos∠ADQ=
;④cos∠ADQ= ![]() ,其中正确结论是(填写序号)
,其中正确结论是(填写序号) 
参考答案:
【答案】①②④
【解析】解:正确结论是①②④. 提示:①连接OQ,OD,如图1.
易证四边形DOBP是平行四边形,从而可得DO∥BP.
结合OQ=OB,可证到∠AOD=∠QOD,从而证到△AOD≌△QOD,
则有DQ=DA=1.
故①正确;②连接AQ,如图2.
则有CP= ![]() ,BP=
,BP= ![]() =
= ![]() .
.
易证Rt△AQB∽Rt△BCP,
运用相似三角形的性质可求得BQ= ![]() ,
,
则PQ= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
故②正确;③过点Q作QH⊥DC于H,如图3.
易证△PHQ∽△PCB,
运用相似三角形的性质可求得QH= ![]() ,
,
∴S△DPQ= ![]() DPQH=
DPQH= ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
故③错误;④过点Q作QN⊥AD于N,如图4.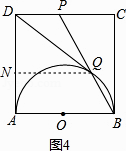
易得DP∥NQ∥AB,
根据平行线分线段成比例可得 ![]() =
= ![]() =
= ![]() ,
,
则有 ![]() =
= ![]() ,
,
解得:DN= ![]() .
.
由DQ=1,得os∠ADQ= ![]() =
= ![]() .
.
故④正确.
综上所述:正确结论是①②④.
所以答案是:①②④.
【考点精析】通过灵活运用平行四边形的判定与性质和平行线分线段成比例,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;三条平行线截两条直线,所得的对应线段成比例即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论: ①2a﹣b=0;
②9a+3b+c<0;
③关于x的一元二次方程ax2+bx+c+3=0有两个相等实数根;
④8a+c<0.
其中正确的个数是( )
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足是G,F是CG的中点,延长AF交⊙O于E,CF=2,AF=3,则EF的长是 .

-
科目: 来源: 题型:
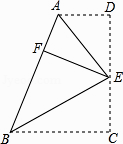
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.

(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
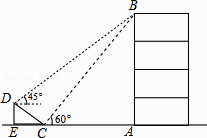
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进A,B两种钢笔,若购进A种钢笔2支,B种钢笔3支,共需90元;购进A种钢笔3支,B种钢笔5支,共需145元.
(1)求A、B两种钢笔每支各多少元?
(2)若该文具店要购进A,B两种钢笔共90支,总费用不超过1588元,并且A种钢笔的数量少于B种钢笔的数量,那么该文具店有哪几种购买方案?
(3)文具店以每支30元的价格销售B种钢笔,很快销售一空,于是,文具店决定在进价不变的基础上再购进一批B种钢笔,涨价卖出,经统计,B种钢笔售价为30元时,每月可卖68支;每涨价1元,每月将少卖4支,设文具店将新购进的B种钢笔每支涨价a元(a为正整数),销售这批钢笔每月获利W元,试求W与a之间的函数关系式,并且求出B种铅笔销售单价定为多少元时,每月获利最大?最大利润是多少元?
相关试题

