【题目】我市为创建“国家级森林城市”,政府决定对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗.某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价及成活率如表:

设购买甲种树苗x棵,承包商获得的利润为y元.请根据以上信息解答下列问题:
(1) 设y与x之间的函数关系式,并写出自变量x的取值范围;
(2) 承包商要获得不低于中标价16%的利润,应如何选购树苗?
(3) 政府与承包商的合同要求,栽植这批树苗的成活率必须不低于93%,否则承包商出资补栽;若成货率达到94%以上(含94%),则政府另给予工程款总额6%的奖励,该承包商应如何选购树苗才能获得最大利润?最大利润是多少?
参考答案:
【答案】(1)、y=12x+20000(0<x≤3000);(2)、购买甲种树苗不少于1800棵且不多于3000棵;(3)、购买甲种树苗1200棵,一种树苗4800棵,可获得最大利润,最大利润是50000元
【解析】
试题分析:(1)、根据利润=26万-总成本得出函数关系式;(2)、根据题意得出不等式,然后求出x的取值范围;(3)、①、当成活率不低于93%且低于94%时得出不等式组,求出x的取值范围,然后根据函数的性质求出最值,②当成活率到达94%以上列出不等式,求出最大值,然后根据两者进行选择.
试题解析:(1)、y=260000-[20x+32(6000-x)+8×6000]=12x+20000
自变量的取值范围是:0<x≤3000;
(2)、由题意,得12x+20000≥260000×16%,解得:x≥1800, ∴1800≤x≤3000,
购买甲种树苗不少于1800棵且不多于3000棵;
、①若成活率不低于93%且低于94%时,由题意得
![]() 解得1200<x≤2400
解得1200<x≤2400
在y=12x+20000中, ∵12>0, ∴y随x的增大而增大,
∴当x=2400时,y最大=48800,
②若成活率达到94%以上(含94%),则0.9x+0.95(6000-x)≥0.94×6000, 解得:x≤1200,
由题意得y=12x+20000+260000×6%=12x+35600, ∵12>0, ∴y随x的增大而增大,
∴当x=1200时,y最大值=5000,
综上所述,50000>48800
∴购买甲种树苗1200棵,一种树苗4800棵,可获得最大利润,最大利润是50000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆外切等腰梯形的一腰长是8,则这个等腰梯形的上底与下底长的和为( )
A.4
B.8
C.12
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的方程2x+k﹣4=0的解是x=﹣3,那么k的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把a2﹣4a多项式分解因式,结果正确的是( )
A. a(a﹣4) B. (a+2)(a﹣2) C. a(a+2)(a﹣2) D. (a﹣2)2﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家环保局统一规定,空气质量分为5级:当空气污染指数达0—50时为1级,质量为优;51—100时为2级,质量为良;101—200时为3级,轻度污染;201—300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:

(1) 本次调查共抽取了 天的空气质量检测结果进行统计;
(2) 补全条形统计图;
(3) 扇形统计图中3级空气质量所对应的圆心角为 °;
(4) 如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2015年该城市有多少天不适宜开展户外活动.(2015年共365天)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点
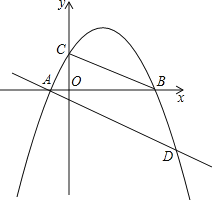
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
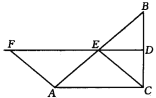
(1)求证:四边形ACEF是平行四边形;
(2)当∠B的大小满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论;
(3)四边形ACEF有可能是正方形吗?为什么?
相关试题

