【题目】E折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 . 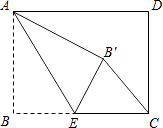
参考答案:
【答案】![]() 或3
或3
【解析】解:当△CEB′为直角三角形时,有两种情况: 
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=3,BC=4,
∴AC= ![]() =5,
=5,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=5﹣3=2,
设BE=x,则EB′=x,CE=4﹣x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2 ,
∴x2+22=(4﹣x)2 , 解得x= ![]() ,
,
∴BE= ![]() ;
;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,∴BE=AB=3.
综上所述,BE的长为 ![]() 或3.
或3.
所以答案是: ![]() 或3.
或3.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
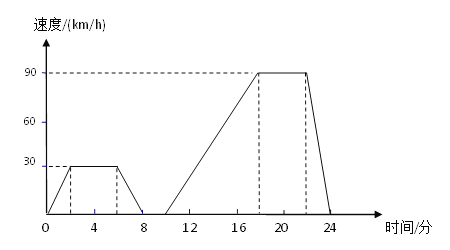
查看答案和解析>>【题目】如图表示的是汽车在行驶的过程中,速度随时间变化而变化的情况.
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在那些时间段保持匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)用自己的语言大致描述这辆汽车的行驶情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:m2﹣4= .
-
科目: 来源: 题型:
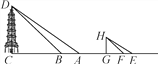
查看答案和解析>>【题目】学习了《相似图形》一章后,小华想测量一座底部不可直接到达的塔DC的高度,上午8点时,测得塔的影子顶端落在地面上的A处,此时小华站在地面上的G处,发现自己的影子顶端落在地面上的E处;上午10点时,测得塔的影子顶端落在地面上的B处,此时站在G处的小华发现自己的影子顶端落在地面上的F处.已知小华身高HG=1.8 m,经测量AB=10 m,FE=0.4 m,求塔DC的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程(m-3)x|m|-2 -m+3=0是一元一次方程,则m的值为( )
A.m=3B.m=-3C.m=3或-3D.m=2或-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列成语所描述的事件,是随机事件的是( )
A. 水涨船高 B. 一箭双雕 C. 水中捞月 D. 一步登天
相关试题

