搜索
【题目】某储运站现有甲种货物1530吨，乙种货物1150吨，安排用一列货车将这批货物运往青岛，这列货车可挂A，B两种不同规格的货厢50节．已知甲种货物35吨和乙种货物15吨可装满一节A型货厢，甲种货物25吨和乙种货物35吨可装满一节B型货厢，按此要求安排A,B两种货厢的节数，有哪几种运输方案？请设计出来．
参考答案：
【答案】见解析
【解析】
由题意可建立不等式组：即A型和B型装的甲种货物不能少于1530吨，A型和B型装的乙种货物不能少于1150吨，设A型x节，则B型就是（50-x）节，列出不等式组求解．
设A型x节，B型（50-x）节，
由题意得
，解得，28≤x≤30，
∴有三种方案：①A：28，B：22；②A：29，B：21；③A：30，B：20；
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校运动会需购买A，B两种奖品，若购买A种奖品3件和B种奖品2件，共需60元；若购买A种奖品5件和B种奖品3件，共需95元．
（1）求A、B两种奖品的单价各是多少元？
（2）学校计划购买A、B两种奖品共100件，购买费用不超过1150元，且A种奖品的数量不大于B种奖品数量的3倍，设购买A种奖品m件，购买费用为W元，写出W（元）与m（件）之间的函数关系式．求出自变量m的取值范围，并确定最少费用W的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O是△ABC的外接圆，∠ABC=45°，OC∥AD，AD交BC的延长线于D，AB交OC于E．
（1）求证：AD是⊙O的切线；
（2）若⊙O的直径为6，线段BC=2，求∠BAC的正弦值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况．他从中随机调查了40户居民家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图．
根据以上提供的信息，解答下列问题：
（1）补全频数分布表．
（2）补全频数分布直方图．
（3）绘制相应的频数分布折线图．
（4）请你估计该居民小区家庭属于中等收入（大于1000不足1600元）的大约有多少户？
-
科目： 来源： 题型：
查看答案和解析>>【题目】冬天来了，晒衣服成了头疼的事情，聪明的小华想到一个好办法，在家后院地面（BD）上立两根等长的立柱AB、CD（均与地面垂直），并在立柱之间悬挂一根绳子．绳子的形状近似成了抛物线
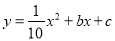，如图1，已知BD=8米，绳子最低点离地面的距离为1米．（1）求立柱AB的长度；
（2）由于挂的衣服比较多，为了防止衣服碰到地面，小华用一根垂直于地面的立柱MN撑起绳子（如图2），MN的长度为1.85米，通过调整MN的位置，使左边抛物线F1对应函数的二次项系数为
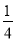，顶点离地面1.6米，求MN离AB的距离．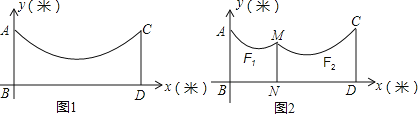
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M在线段OA和射线AC上运动．
（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）是否存在点M，使△OMC的面积是△OAC的面积的
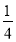？若存在求出此时点M的坐标；若不存在，说明理由．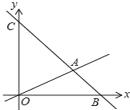
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，抛物线
交y轴于点A，交直线x=6于点B.（1）填空：抛物线的对称轴为x=_________，点B的纵坐标为__________（用含a的代数式表示）；
（2）若直线AB与x轴正方向所夹的角为45°时，抛物线在x轴上方，求
的值；（3）记抛物线在A、B之间的部分为图像G（包含A、B两点），若对于图像G上任意一点
，总有
≤3，求a的取值范围.
相关试题
