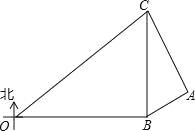
【题目】在某次海上军事学习期间,我军为确保△OBC海域内的安全,特派遣三艘军舰分别在O、B、C处监控△OBC海域,在雷达显示图上,军舰B在军舰O的正东方向80海里处,军舰C在军舰B的正北方向60海里处,三艘军舰上装载有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域.(只考虑在海平面上的探测)
(1)若三艘军舰要对△OBC海域进行无盲点监控,则雷达的有效探测半径r至少为多少海里?
(2)现有一艘敌舰A从东部接近△OBC海域,在某一时刻军舰B测得A位于北偏东60°方向上,同时军舰C测得A位于南偏东30°方向上,求此时敌舰A离△OBC海域的最短距离为多少海里?
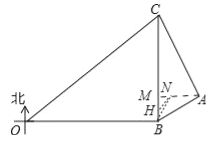
(3)若敌舰A沿最短距离的路线以20![]() 海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
参考答案:
【答案】(1)雷达的有效探测半径r至少为50海里;(2)敌舰A离△OBC海域的最短距离为15![]() 海里;(3)B军舰速度至少为20海里/小时.
海里;(3)B军舰速度至少为20海里/小时.
【解析】
试题分析:(1)在RT△OBC中,根据勾股定理求出OC,由题意r≥![]() OC,由此得答案.(2)作AM⊥BC于M,先求得AB的长,在RT△ABM中求出AM的长即可得答案.(3)假设B军舰在点N处拦截到敌舰.在BM上取一点H,使得HB=HN,设MN=x,先列出方程求出x,再求出BN、AN利用不等式解决问题.
OC,由此得答案.(2)作AM⊥BC于M,先求得AB的长,在RT△ABM中求出AM的长即可得答案.(3)假设B军舰在点N处拦截到敌舰.在BM上取一点H,使得HB=HN,设MN=x,先列出方程求出x,再求出BN、AN利用不等式解决问题.
试题解析:(1)在RT△OBC中,∵BO=80,BC=60,∠OBC=90°,
∴OC=![]() ,
,
∵![]() OC=
OC=![]() ×100=50
×100=50
∴雷达的有效探测半径r至少为50海里.
(2)作AM⊥BC于M,
∵∠ACB=30°,∠CBA=60°,
∴∠CAB=90°,
∴AB=![]() BC=30,
BC=30,
在RT△ABM中,∵∠AMB=90°,AB=30,∠BAM=30°,
∴BM=![]() AB=15,AM=
AB=15,AM=![]() BM=15
BM=15![]() ,
,
∴此时敌舰A离△OBC海域的最短距离为15![]() 海里.
海里.
(3)假设B军舰在点N处拦截到敌舰.在BM上取一点H,使得HB=HN,设MN=x,
∵∠HBN=∠HNB=15°,
∴∠MHN=∠HBN+∠HNB=30°,
∴HN=HB=2x,MH=![]() x,
x,
∵BM=15,
∴15=![]() x+2x,
x+2x,
x=30﹣15![]() ,
,
∴AN=30![]() ﹣30,
﹣30,
BN=![]() ,设B军舰速度为a海里/小时,
,设B军舰速度为a海里/小时,
由题意![]() ,
,
∴a≥20.
∴B军舰速度至少为20海里/小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据3,3,3,3,3,那么这组数据的方差为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级有452名学生,为了了解这452名学生的课外阅读情况,从中抽取50名学生进行统计.在这个问题中,样本是( )
A.452名学生B.抽取的50名学生
C.452名学生的课外阅读情况D.抽取的50名学生的课外阅读情况
-
科目: 来源: 题型:
查看答案和解析>>【题目】福州地铁将于2014年12月试通车,规划总长约180000米,用科学记数法表示这个总长为( )
A.0.18×106米
B.1.8×106米
C.1.8×105米
D.18×104米 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:5x2x4﹣(﹣2x3)2+x8÷x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角坐标系中,点P(x,y)在第二象限,且P到x轴、y轴的距离分别为4、5,则点P的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
相关试题

