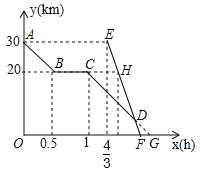
【题目】周末,小芳骑自行车从家出发到野外郊游,从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地,小芳离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地,如图是她们距乙地的路程y(km)与小芳离家时间x(h)的函数图象.
(1)小芳骑车的速度为 km/h,H点坐标 .
(2)小芳从家出发多少小时后被妈妈追上?此时距家的路程多远?
(3)相遇后,妈妈载上小芳和自行车同时到达乙地(彼此交流时间忽略不计),求小芳比预计时间早几分钟到达乙地?

参考答案:
【答案】(1)20,H(![]() ,20);(2)小芳出发1.75小时候被妈妈追上,此时距家25km;(3)10.
,20);(2)小芳出发1.75小时候被妈妈追上,此时距家25km;(3)10.
【解析】试题分析:(1)根据函数图中的数据,由小芳从家到甲地的路程和时间可以求出小芳骑车的速度;
(2)先求出直线AB的解析式,再根据直线AB∥CD,求出直线CD的解析式,再求出直线EF的解析式,联立直线CD和直线EF的解析式,求出交点D的坐标即可;
(3)将y=0,分别代入直线CD和直线EF的解析式,分别求出求出当y=0时候的横坐标,再求出两横坐标的差值即可.
试题解析:(1)由函数图可以得出,小芳家距离甲地的路程为10km,花费时间为0.5h,故小芳骑车的速度为:10÷0.5=20(km/h),由题意可得出,点H的纵坐标为20,横坐标为: ![]() =
=![]() ,故点H的坐标为(
,故点H的坐标为(![]() ,20);
,20);
(2)设直线AB的解析式为:y1=k1x+b1,将点A(0,30),B(0.5,20)代入得:y1=﹣20x+30,∵AB∥CD,∴设直线CD的解析式为:y2=﹣20x+b2,将点C(1,20)代入得:b2=40,故y2=﹣20x+40,设直线EF的解析式为:y3=k3x+b3,将点E(![]() ,30),H(
,30),H(![]() ,20)代入得:k3=﹣60,b3=110,∴y3=﹣60x+110,解方程组
,20)代入得:k3=﹣60,b3=110,∴y3=﹣60x+110,解方程组![]() ,得
,得![]() ,∴点D坐标为(1.75,5),30﹣5=25(km),所以小芳出发1.75小时候被妈妈追上,此时距家25km;
,∴点D坐标为(1.75,5),30﹣5=25(km),所以小芳出发1.75小时候被妈妈追上,此时距家25km;
(3)将y=0代入直线CD解析式有:﹣20x+40=0,解得x=2,将y=0代入直线EF的解析式有:﹣60x+110=0,解得x=![]() ,2﹣
,2﹣![]() =
=![]() (h)=10(分钟),故小芳比预计时间早10分钟到达乙地.
(h)=10(分钟),故小芳比预计时间早10分钟到达乙地.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师到市教育局大楼办事,他从一楼出发,要去不同楼层办理具体事务,如果约定乘电梯向上一楼记作+1,向下一楼记作-1,那么李老师办事过程中电梯上下楼层依次记录如下:+6,-3,+9,-5,-7.(单位:层)
(1)请说明李老师是否在十三楼办理过事务?
(2)请说明李老师最后是否回到出发点一楼?
(3)该大楼每层高3m,电梯每向上或向下1m大约需要耗电0.01度,请你算算,他办事中电梯需要耗电多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和加上它的外角和等于900°,求此多边形的边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是()
组别
A型
B型
C型
O型
频率
0.4
0.35
0.1
0.15
A.16人B.14人C.4人D.6人
-
科目: 来源: 题型:
查看答案和解析>>【题目】某个体户购进一批时令水果,20天销售完毕,他将本次销售情况进行了跟踪记录,根据所记录的数据绘制如下的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图(1)所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图(2)所示。(销售额=销售单价×销售量)
(1)直接写出y与x之间的函数解析式;
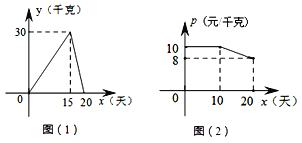
(2)分别求第10天和第15天的销售额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中,“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是
A.两直线被第三条直线所截得的同位角相等
B.两直线被第三条直线所截得的同旁内角互补
C.两平行线被第三条直线所截得的同位角的平分线互相垂直
D.两平行线被第三条直线所截得的同旁内角的平分线互相垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题的逆命题是假命题的是( )
A.两直线平行,同位角相等B.等腰三角形两底角相等
C.两三角形全等,三对对应边相等D.相反数的绝对值相等
相关试题

