【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F . 过点E作EG∥BC , 交AB于G , 则图中相似三角形有( ) 
A.4对
B.5对
C.6对
D.7对
参考答案:
【答案】B
【解析】解答:图中相似三角形有△ABC∽△CDA , △AGE∽△ABC , △AFE∽△CBE , △BGE∽△BAF , △AGE∽△CDA共5对, 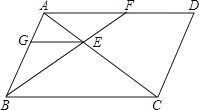
理由是:∵四边形ABCD是平行四边形,
∴AD∥BC , AB∥CD , AD=BC , AB=CD , ∠D=∠ABC ,
∴△ABC≌△CDA , 即△ABC∽△CDA ,
∵GE∥BC ,
∴△AGE∽△ABC∽△CDA ,
∵GE∥BC , AD∥BC ,
∴GE∥AD ,
∴△BGE∽△BAF ,
∵AD∥BC ,
∴△AFE∽△CBE .
故选B .
分析:根据平行四边形的性质得出AD∥BC , AB∥CD , AD=BC , AB=CD , ∠D=∠ABC , 推出△ABC≌△CDA , 即可推出△ABC∽△CDA , 根据相似三角形的判定定理:平行于三角形一边的直线截其它两边或其它两边的延长线,所截的三角形与原三角形相似即可推出其它各对三角形相似.
【考点精析】掌握相似三角形的判定是解答本题的根本,需要知道相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件,不能判定△ABC与△DEF相似的是( )
A.∠C=∠F=90°,∠A=55°,∠D=35°
B.∠C=∠F=90°,AB=10,BC=6,DE=15,EF=9
C.∠C=∠F=90°,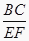 =
= 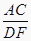
D.∠B=∠E=90°,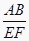 =
= 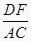
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角△ABC中,BE , CD是高,它们相交于O , 则图中与△BOD相似的三角形有( )
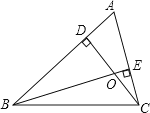
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列4组条件中,能判定△ABC∽△DEF的是( )
A.AB=5,BC=4,∠A=45°;DE=10,EF=8,∠D=45°
B.∠A=45°,∠B=55°;∠D=45°,∠F=75°
C.BC=4,AC=6,AB=9;DE=18,EF=8,DF=12
D.AB=6,BC=5,∠B=40°;DE=5,EF=4,∠E=40° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB延长线于E , 则图中一定相似的三角形是( )

A.△AED与△ACB
B.△AEB与△ACD
C.△BAE与△ACE
D.△AEC与△DAC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是直角△ABC (∠C=90°)的角平分线,EF⊥AD于D , 与AB及AC的延长线分别交于E , F , 写出图中的一对全等三角形是 ;一对相似三角形是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在Rt△ABC中∠C=90°,CD为AB边上的高. 求证:Rt△ADC∽Rt△CDB .

相关试题

