【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图: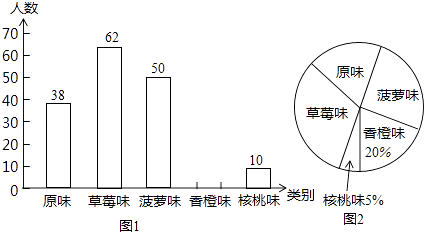
(1)本次被调查的学生有名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
参考答案:
【答案】
(1)解:10÷5%=200(名)答:本次被调查的学生有200名,故答案为:200;
(2)解:200﹣38﹣62﹣50﹣10=40(名),
条形统计图如下:
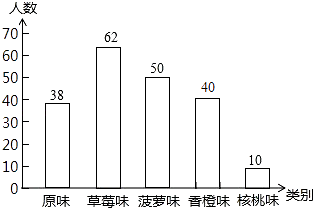
![]() =90°,
=90°,
答:喜好“菠萝味”牛奶的学生人数在扇形统计图2中所占圆心角的度数为90°
(3)解:1200×( ![]() )=144(盒),
)=144(盒),
答:草莓味要比原味多送144盒
【解析】(1)喜好“核桃味”牛奶的学生人数除以它所占的百分比即可得本次被调查的学生人数;
(2)用本次被调查的学生的总人数减去喜好原味、草莓味、菠萝味、核桃味的人数得出喜好香橙味的人数,补全条形统计图即可,用喜好“菠萝味”牛奶的学生人数除以总人数再乘以360°,即可得喜好“菠萝味”牛奶的学生人数在扇形统计图2中所占圆心角的度数;
(3)用喜好草莓味的人数占的百分比减去喜好原味的人数占的百分比,再乘以该校的总人数即可.
-
科目: 来源: 题型:
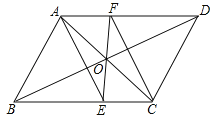
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由.
-
科目: 来源: 题型:
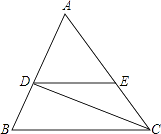
查看答案和解析>>【题目】如图,已知DE∥BC,CD是∠ACB的平分线,∠B=70°,∠ACB=50°,求∠EDC和∠BDC的度数.
-
科目: 来源: 题型:
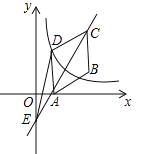
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线
 (k≠0,x>0)过点D.
(k≠0,x>0)过点D.(1)求双曲线的解析式;
(2)作直线AC交y轴于点E,连结DE,求△CDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】回答下列问题
(1)问题发现 如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.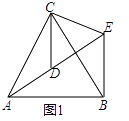
(2)拓展探究 如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.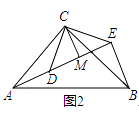
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(-1, 2),将它先向左平移2个单位,再向上平移3个单位后得到点B,则点B的坐标是________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形?(不需说明理由)
(2)如果AM=1,sin∠DMF=
 ,求AB的长.
,求AB的长.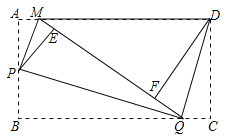
相关试题

