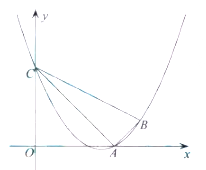
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
(1)求此二次函数的关系式;
(2)判断![]() 的形状;若
的形状;若![]() 的外接圆记为
的外接圆记为![]() ,请直接写出圆心
,请直接写出圆心![]() 的坐标;
的坐标;
(3)若将抛物线沿射线![]() 方向平移,平移后点
方向平移,平移后点![]() 、
、![]() 、
、![]() 的对应点分别记为点
的对应点分别记为点![]() 、
、![]() 、
、![]() ,
,![]() 的外接圆记为
的外接圆记为![]() ,是否存在某个位置,使
,是否存在某个位置,使![]() 经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.
经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)直角三角形,(2,2)(3)存在,抛物线的关系式为
(2)直角三角形,(2,2)(3)存在,抛物线的关系式为
![]() 或
或![]()
【解析】
试题分析:(1)根据待定系数法可直接代入得到方程组求值,得到函数的解析式;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,然后根据角之间的关系得到是直角三角形,最后根据坐标得到D点;
,然后根据角之间的关系得到是直角三角形,最后根据坐标得到D点;
(3)取![]() 中点
中点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,根据勾股定理求出MC的长和OM的长,再通过平移的性质得到平移的距离,然后根据二次函数的平移性质可得到解析式.
,根据勾股定理求出MC的长和OM的长,再通过平移的性质得到平移的距离,然后根据二次函数的平移性质可得到解析式.
试题解析:(1)把点![]() ,
,![]() 代入
代入![]() 中得
中得
![]() ,解得
,解得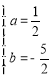 ,
,
所以所求函数的关系式为![]() .
.
(2)![]() 为直角三角形.
为直角三角形.
过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
易知点![]() 坐标为
坐标为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又因为点![]() 坐标为
坐标为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() 为直角三角形,
为直角三角形,
圆心![]() 的坐标为
的坐标为![]() .
.
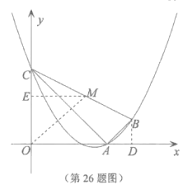
(3)存在.
取![]() 中点
中点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
因为![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
所以要使抛物线沿射线![]() 方向平移,
方向平移,
且使![]() 经过原点,
经过原点,
则平移的长度为![]() 或
或![]() ,
,
因为![]() ,
,
所以抛物线的顶点向左、向下均分别平移![]() 个单位长度,
个单位长度,
或![]() 个单位长度.
个单位长度.
因为![]() .
.
所以平移后抛物线的关系式为![]() ,
,
即![]()
或![]() ,即
,即![]() .
.
综上所述,存在一个位置,使![]() 经过原点,此时抛物线的关系式为
经过原点,此时抛物线的关系式为
![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=﹣2(x+1)2﹣2向左平移2个单位,向下平移3个单位后的新抛物线解析式为( )
A. y=﹣2(x﹣1)2+1B. y=﹣2(x+3)2﹣5
C. y=﹣2(x﹣1)2﹣5D. y=﹣2(x+3)2+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间每天能制作甲种零件200只,或者制作乙种零件150只,2只甲种零件与3只乙种零件配成一套产品,现要在30天内制作最多的成套产品,则甲、乙两种零件各应制作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(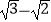 )0﹣(﹣
)0﹣(﹣  )2÷2﹣2﹣(﹣1)3
)2÷2﹣2﹣(﹣1)3
(2)(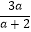
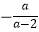 )
) 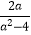 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,湿地景区岸边有三个观景台
 、
、 、
、 .已知
.已知 米,
米, 米,
米, 点位于
点位于 点的南偏西
点的南偏西 方向,
方向, 点位于
点位于 点的南偏东
点的南偏东 方向.
方向.(1)求
 的面积;
的面积;(2)景区规划在线段
 的中点
的中点 处修建一个湖心亭,并修建观景栈道
处修建一个湖心亭,并修建观景栈道 .试求
.试求 、
、 间的距离.(结果精确到
间的距离.(结果精确到 米)
米)(参考数据:
 ,
, ,
, ,
, ,
, ,
, ,
, )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:9+(﹣6)的结果为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤,设安排
 名工人采摘蓝莓,剩下的工人加工蓝莓.
名工人采摘蓝莓,剩下的工人加工蓝莓.(1)若基地一天的总销售收入为
 元,求
元,求 与
与 的函数关系式;
的函数关系式;(2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值.
相关试题

