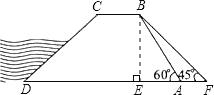
【题目】如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60°,坡长AB=20![]() m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据:
m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据:![]() 1.414,
1.414,![]() 1.732).
1.732).

参考答案:
【答案】AF的长约为13米.
【解析】
试题分析:过B作DF的垂线,设垂足为E;可在Rt△ABE中,根据坡面AB的长以及坡角的度数,求得铅直高度BE和水平宽AE的值,进而可在Rt△BFE中,根据BE的长及坡角的度数,通过解直角三角形求出EF的长;根据AF=EF﹣AE,即可得出AF的长度.
解:过B作BE⊥DF于E.
Rt△ABE中,AB=20![]() m,∠BAE=60°,
m,∠BAE=60°,
∴BE=ABsin60°=20![]() ×
×![]() =30,
=30,
AE=ABcos60°=20![]() ×
×![]() =10
=10![]() .
.
Rt△BEF中,BE=30,∠F=45°,
∴EF=BE=30.
∴AF=EF﹣AE=30﹣10![]() ≈13,
≈13,
即AF的长约为13米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较大小:﹣4________﹣2,4的相反数是________.﹣5的倒数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆心在坐标原点的⊙O的半径为1,若抛物线y=﹣x2+c和⊙O刚好有三个公共点,则此时c= .若抛物线和⊙O只有两个公共点,则c可以取的一切值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知抛物线y=﹣
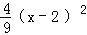 +c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
+c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=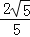 .
.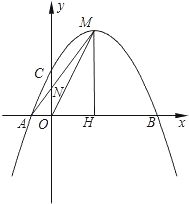
(1)求此抛物线的函数表达式;
(2)过H的直线与y轴相交于点P,过O,M两点作直线PH的垂线,垂足分别为E,F,若
 =
= 时,求点P的坐标;
时,求点P的坐标;(3)将(1)中的抛物线沿y轴折叠,使点A落在点D处,连接MD,Q为(1)中的抛物线上的一动点,直线NQ交x轴于点G,当Q点在抛物线上运动时,是否存在点Q,使△ANG与△ADM相似?若存在,求出所有符合条件的直线QG的解析式;若不存在,请说明理由.
-
科目: 来源: 题型:
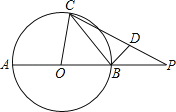
查看答案和解析>>【题目】如图,AB是⊙O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC上.设∠PCB=α,∠POC=2β.求证:tanαtanβ=
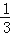 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=4,BC=3,以C为圆心,CB的长为半径的圆和AC交于点D,连接BD,若∠ABD=
 ∠C.
∠C.
(1)求证:AB是⊙C的切线;
(2)求△DAB的面积.
相关试题

