【题目】如图,在△ABC中,AD⊥BC于D, CE平分∠ACB分别交AB、AD于E、F两点,且BD=FD,AB=CF.求证:(1)CE![]() AB;(2)AE=BE.
AB;(2)AE=BE.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据直角三角形的全等证明和全等三角形的性质解答即可;
(2)根据角平分线的性质和全等三角形的判定和性质证明即可.
试题解析:证明:(1)∵AD⊥BC于D,∴∠ADB=∠CDF=90°.在Rt△ADB和Rt△CDF中,∵AB=CF,BD=DF,∴Rt△ADB≌Rt△CDF(HL),∴∠BAD=∠DCF.在△AEF和△CDF中,∠EAF=∠DCF,∠AFE=∠CFD,∴∠AEC=∠CDF=90°,∴CE⊥AB;
(2)∵CE平分∠ACB,∴∠ACE=∠BCE.又∵CE⊥AB,∴∠AEC=∠BEC=90°.在△ACE和△BCE中,∠ACE=∠BCE,CE=CE,∠AEC=∠BEC,∴△ACE≌△BCE(ASA),∴AE=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为洪涛同学的小测卷(每小题25分,共100分),他的得分应是______分.
姓名 洪涛 得分?
填空
①2的相反数是 -2 ;
②倒数等于它本身的数是1和-1;
③-1的绝对值是 1 ;
④2的立方是 6 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
利用完全平方公式,可以将多项式
 变形为
变形为 的形式, 我们把这样的变形方法叫做多项式
的形式, 我们把这样的变形方法叫做多项式 的配方法.运用多项式的配方法及平方差公式能对一些多项式进行分解因式.例如:
的配方法.运用多项式的配方法及平方差公式能对一些多项式进行分解因式.例如:  =
=
=

=
 =
=
根据以上材料,解答下列问题:
(1)用多项式的配方法将
 化成
化成 的形式;
的形式;
(2)下面是某位同学用配方法及平方差公式把多项式
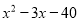 进行分解因式的解答过程:
进行分解因式的解答过程:老师说,这位同学的解答过程中有错误,请你找出该同学解答中开始出现错误的地方,并用“ ”标画出来,然后写出完整的、正确的解答过程:
(3)求证:x,y取任何实数时,多项式
 的值总为正数.
的值总为正数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知:
 ,
,  求作:
求作:  ,使得
,使得 ,
,  .
. 作图:
作图:(2)如图,已知
 ,求作射线OC,使OC平分
,求作射线OC,使OC平分 .
.作射线OC;
在OA和OB上分别截取OD,OE,使OD=OE;
分别以点D,E为圆心,以大于
 长为半径,
长为半径,在
 内作弧,两弧交于点C.上述做法合理的顺序是_____________.(写序号)
内作弧,两弧交于点C.上述做法合理的顺序是_____________.(写序号)
这样做出的射线OC就是∠O 的角平分线,其依据是___________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法对31500取近似数,精确到千位,用科学计数法可表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,1980年世界人口的分布状况是:亚洲25.8亿人,欧洲7.5亿人,非洲4.6亿人,拉丁美洲3.5亿人,北美洲2.4亿人,大洋洲0.2亿人,全球合计44.0亿人.
(1)请制作一张统计图描述以上统计数据.
(2)请根据统计表格中的数据制作扇形统计图.
(3)从以上统计图、表中,你能得到哪些信息.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.

相关试题

