【题目】阅读材料:
我们知道|x|=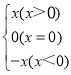 ,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x-2|时,可令x+1=0和x-2=0,分别求得x=-1,x=2(称-1,2分别为|x+1|与|x-2|的零点值),在实数范围内,零点值x=-1和x=2可将全体实数分成不重复且不遗漏的如下3种情况:
,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x-2|时,可令x+1=0和x-2=0,分别求得x=-1,x=2(称-1,2分别为|x+1|与|x-2|的零点值),在实数范围内,零点值x=-1和x=2可将全体实数分成不重复且不遗漏的如下3种情况:
(1)当x<-1时,原式=-(x+1)-(x-2)=-2x+1;
(2)当-1≤x<2时,原式=x+1-(x-2)=3;
(3)当x≥2时,原式=x+1+x-2=2x-1.综上所述,原式=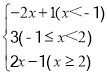
学以致用:
(Ⅰ)分别求出|x+3|和|x-1|的零点值;
(Ⅱ)化简代数式|x+3|+|x-1|;
拓展应用:
(Ⅲ)求函数y=|x+3|+|x-1|(-3≤x≤3)的最大值和最小值.
参考答案:
【答案】(1)零点值分别为-3和1;(2)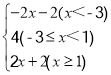 ;(3)最大值是8和最小值是4.
;(3)最大值是8和最小值是4.
【解析】
试题分析:(Ⅰ)阅读材料,根据零点值的求法,即绝对值里面的代数式等于0,即可解答;
(Ⅱ)根据阅读材料中,化简带绝对值的代数式的方法,根据x的取值范围,分为三种情况,根据绝对值的性质解答即可;
(Ⅲ)分x<-3、-3≤x≤1、x>1分别化简,结合x的取值范围确定代数式值的范围,从而求出函数的最值.
试题解析:(Ⅰ)令x+3=0和x-1=0,分别求得x=-3,x=1,
所以|x+3|和|x-1|的零点值分别为-3和1;
(Ⅱ)在实范围内,零点值x=-3和x=1可将全体实数分成不重复且不遗漏的如下3种情况:
(1)当x<-3时,原式=-(x+3)-(x-1)=-2x-2;
(2)当-3≤x<1时,原式=(x+3)-(x-1)=4;
(3)当x≥1时,原式=x+3+x-1=2x+2.
综上所述,原式=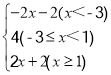 ;
;
(Ⅲ)由(Ⅱ)可化简函数为y=![]() .
.
该函数的大致图形如图所示:
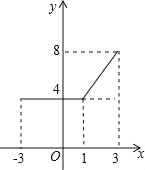
所以函数y=|x+3|+|x-1|(-3≤x≤3)的最大值是8和最小值是4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 下面两个多位数1248624……、6248624……,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位。对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的。当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x-1)(x+1)=1-x的解是( )
A. x=1 B. x=-1
C. x=1或x=-2 D. x=-1或 x=-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片
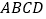 沿对角线
沿对角线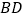 折叠,点
折叠,点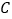 落在点
落在点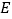 处,
处,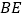 交
交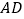 于点
于点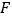 ,连结
,连结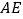 .证明:(1)BF=DF.(2)若BC=8,DC=6,求BF的长。
.证明:(1)BF=DF.(2)若BC=8,DC=6,求BF的长。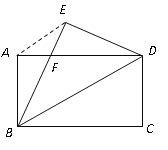
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中,△ABC 的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点P. 若点P向右平移x个单位长度后落在△A2B2C2的内部(不含落在△A2B2C2的边上),请直接写出x的取值范围..
(提醒:每个小正方形边长为1个单位长度)

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次考试中以某个分数为标准,超过记为正,不足记为负,小明的分数记为”+5”, 小华的分数记为”-3”,两人的分数之和是180分,小华考了______分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有9名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前4名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的( )
A.中位数
B.众数
C.平均数
D.加权平均数
相关试题

