【题目】如图,已知二次函数 ![]() 的图像经过点A(-1,-1)和点B(3,-9).
的图像经过点A(-1,-1)和点B(3,-9).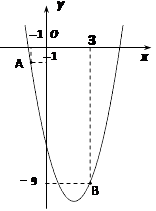
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m , m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
参考答案:
【答案】
(1)解:将A(﹣1,﹣1)和点B(3,﹣9)代入y=ax2﹣4x+c,
得 ![]() 解得
解得 ![]() ,
,
所以二次函数的表达式为y=x2﹣4x﹣6
(2)解:由y=x2﹣4x﹣6=(x﹣2)2﹣10可知:
对称轴为x=2;顶点坐标为(2,﹣10)
(3)解:将P(m,m)坐标代入y=x2﹣4x﹣6,得m=m2﹣4m﹣6.
解得m1=﹣1,m2=6.
因为m>0,所以m=﹣1不合题意,舍去.所以m=6,
所以P点坐标为(6,6);
因为点P与点Q关于对称轴x=2对称,所以点Q到x轴的距离为46.
【解析】(1)利用待定系数法将点A、点B的坐标代入函数解析式即可求出结果。
(2)利用配方法将函数解析式化成顶点式,即可求出结果。
(3)将点P的坐标代入函数解析式,得出关于m的一元二次方程,解方程求解,根据题意确定m的值,再根据二次函数的对称性求出点Q的坐标。
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一蓄水池有水40m3,按一定的速度放水,水池里的水量y(m3)与放水时间t(分)有如下关系:
放水时间(分)
1
2
3
4
…
水池中水量(m3)
38
36
34
32
…
下列结论中正确的是( )
A. y随t的增加而增大
B. 放水时间为15分钟时,水池中水量为8m3
C. 每分钟的放水量是2m3
D. y与t之间的关系式为y=40t
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
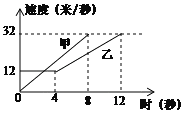
A. 乙前4秒行驶的路程为48米 B. 两车到第3秒时行驶的路程相等
C. 在0到8秒内甲的速度每秒增加4米/秒 D. 在4至8秒内甲的速度都大于乙的速度
-
科目: 来源: 题型:
查看答案和解析>>【题目】清明节假期的某天,小强骑车从家出发前往革命烈士陵园扫墓,匀速行驶一段时间后,因车子出现问题,途中耽搁了一段时间,车子修好后,以更快的速度匀速前行,到达烈士陵园扫完墓后匀速骑车回家.其中
 表示小强从家出发后的时间,
表示小强从家出发后的时间, 表示小强离家的距离,下面能反映变量
表示小强离家的距离,下面能反映变量 与
与 之间关系的大致图象是( )
之间关系的大致图象是( )A.
 B.
B. 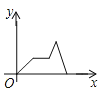
C.
 D.
D. 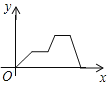
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于
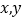 的二元一次方程组
的二元一次方程组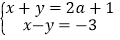 的解都为正数.
的解都为正数.(1)求a的取值范围;
(2)若上述方程组的解是等腰三角形的腰和底边的长,且这个等腰三角形周长为9,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,直线
 ,另一直线交
,另一直线交 于
于 ,交
,交 于
于 ,且
,且 ,点
,点 为直线
为直线 上一动点,点
上一动点,点 为直线
为直线 上一动点,且
上一动点,且 .
.(
 )如图
)如图 ,当点
,当点 在点
在点 右边且点
右边且点 在点
在点 左边时,
左边时, 的平分线交
的平分线交 的平分线于点
的平分线于点 ,求
,求 的度数;
的度数;(
 )如图
)如图 ,当点
,当点 在点
在点 右边且点
右边且点 在点
在点 右边时,
右边时, 的平分线交
的平分线交 的平分线于点
的平分线于点 ,求
,求 的度数;
的度数;(
 )当点
)当点 在点
在点 左边且点
左边且点 在点
在点 左边时,
左边时, 的平分线交
的平分线交 的平分线所在直线交于点
的平分线所在直线交于点 ,请直接写出
,请直接写出 的度数,不说明理由.
的度数,不说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.

(1)试说明:AD∥BC;
(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.
相关试题

