【题目】如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨千米),铁路运价为1.2元/(吨千米),这两次运输共支出公路运费15 000元,铁路运费97200元. 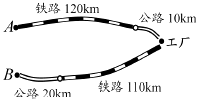
(1)求化工厂从A地购买这批原料及利用这批原料生产的产品各多少吨?
(2)计算这批产品的销售款比原料费和运输费的和多多少元?
参考答案:
【答案】
(1)解:设工厂从A地购买了x吨原料,利用这批原料生产的产品有y吨,
依题意得: ![]() ,
,
整理得: ![]() ,
,
解得: ![]() ,
,
答:工厂从A地购买了400吨原料,利用这批原料生产的产品有300吨
(2)解:依题意得:300×8000﹣400×1000﹣15000﹣97200=1887800(元),
答:这批产品的销售款比原料费与运输费的和多1887800元
【解析】(1)设工厂从A地购买了x吨原料,利用这批原料生产的产品y吨,利用两个等量关系:A地到长青化工厂的公路里程×1.5x+B地到长青化工厂的公路里程×1.5y=这两次运输共支出公路运输费15000元;A地到长青化工厂的铁路里程×1.2x+B地到长青化工厂的铁路里程×1.2y=这两次运输共支出铁路运输费97200元,列出关于x与y的二元一次方程组,求出方程组的解得到x与y的值,即可得到该工厂从A地购买原料的吨数以及制成运往B地的产品的吨数;(2)由第一问求出的原料吨数×每吨1000元求出原料费,再由这两次运输共支出公路运输费15000元,铁路运输费97200元,两运费相加求出运输费之和,由制成运往B地的产品的吨数×每吨8000元求出销售款,最后由这批产品的销售款﹣原料费﹣运输费的和,即可求出所求的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】0.0021用科学记数法表示为( )
A. 2.1×10﹣2B. 2.1×10﹣3C. 2.1×10﹣4D. 21×10﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把(﹣5)﹣(﹣6)+(﹣5)﹣(﹣4)写成省略加号和括号的形式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】 (10分)已知抛物线
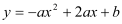 与
与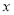 轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
轴的一个交点为A(-1,0),与y轴的正半轴交于点C.(1)直接写出抛物线的对称轴,及抛物线与
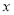 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;(2)当点C在以AB为直径的⊙P上时,求抛物线的解析式;
(3)坐标平面内是否存在点
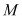 ,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点
,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点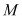 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.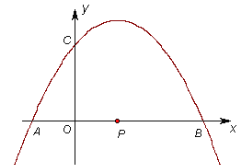
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种饮料重约300g,罐上注有“蛋白质含量≥0.5%”,其中蛋白质的含量为多少克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】夏季来临,商场准备购进甲、乙两种空调,已知甲种空调每台进价比乙种空调多500元,用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同.请解答下列问题:
(1)求甲、乙两种空调每台的进价;
(2)若甲种空调每台售价2500元,乙种空调每台售价1800元,商场计划用不超过36000元购进空调共20台,且全部售出,请写出所获利润y(元)与甲种空调x(台)之间的函数关系式,并求出所能获得的最大
利润.
相关试题

