Question

【题目】如图，在△ABC中，∠ACB=90°，AC=2，BC=4，D、E分别是边AB、BC的中点，点P从点C出发，沿线段CD方向以每秒1个单位长度的速度运动，当点P与点D不重合时，以EP、ED为邻边作EDFP，设点P的运动时间为t（秒）．

（1）求AB长．

（2）当∠DPF=∠PFD时，求t的值．

（3）当点P在线段CD上时，设EDFP与△ABC重叠部分图形的面积为y（平方单位），求y与t之间的函数关系式．

（4）连结AF，当△AFD的面积与△PDE的面积相等时，直接写出t的值．

Answer 1

【答案】(1)10；（2）．(3) y=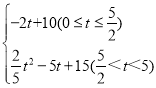．(4) 0或.

【解析】

试题分析：（1）在RT△ABC中利用勾股定理即可解决问题．

（2）如图1中，当∠DPF=∠PFD时，可以证明PE∥AB，PC=PD，由此即可解决问题．

（3）分两种情形①当0≤t≤时，如图2中，作PM⊥DE存在为M，此时重叠部分面积就是平行四边形PEDF的面积，②当＜t＜5时，如图3中，此时y=S△PHD+S△PDE．

（4）两种情形①t=O时，△ADF与△PDE面积相等．②如图4中，当A、P、E共线时△ADF与△PDE面积相等，由DE∥AC得，求出PC即可．

试题解析：（1）在△ABC中，∵∠ACB=90°，AC=2，BC=4，

∴AB=．

（2）如图1中，

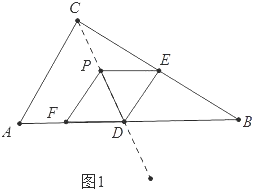
∵四边形PEDF是平行四边形，

∴PF∥DE，PE∥DF，

∴∠DPF=∠PDE，

∵∠ACB=90°，AD=DB，

∴CD=DB=DA=5，∵CE=EB，

∴DE⊥BC，∠CDE=∠EDB

∵∠DPF=∠PFD，

∴∠PED=∠BDE，

∴PE∥DB，∵CE=EB，

∴PC=PD=，

∴t=．

（3）①当0≤t≤时，如图2中，

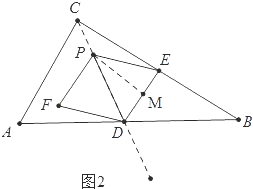
作PM⊥DE存在为M，

∵PM∥CE，

∴，

∴，

∴PM=（5-t），

∴y=DEPM=（5-t）=-2t+10．

②当＜t＜5时，如图3中，

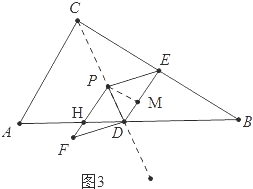
∵PH∥AC，

∴，

∴，

∴H=（5-t），

∴y=S△PHD+S△PDE=PHPM+（-2t+10）=t2-5t+15，

综上所述：y=．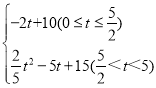

（4）①t=O时，△ADF与△PDE面积相等．

②如图4中，

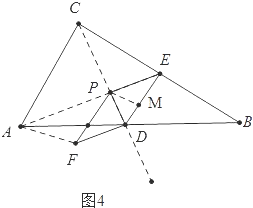
当A、P、E共线时，∵AE∥DF，

∴S△ADF=S△PDF=S△PED，

∵DE∥AC，

∴，

∴PC=，

∴t=，

∴t=0或时，△ADF与△PDE面积相等．