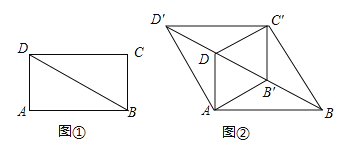
【题目】如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②.
(1)求证:四边形AB'C'D是菱形;
(2)四边形ABC'D′的周长为 ;
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
参考答案:
【答案】(1)证明见解析;(2)4![]() ;(3)6+
;(3)6+![]() 或2
或2![]() +3.
+3.
【解析】
试题分析:(1)有一组邻边相等的平行四边形是菱形,据此进行证明即可;
(2)先判定四边形ABC'D'是菱形,再根据边长AB=![]() AD=
AD=![]() ,即可得到四边形ABC'D′的周长为4
,即可得到四边形ABC'D′的周长为4![]() ;
;
(3)根据两种不同的拼法,分别求得可能拼成的矩形周长
试题解析:(1)∵BD是矩形ABCD的对角线,∠ABD=30°,
∴∠ADB=60°,
由平移可得,B'C'=BC=AD,∠D'B'C'=∠DBC=∠ADB=60°,
∴AD∥B'C'
∴四边形AB'C'D是平行四边形,
∵B'为BD中点,
∴Rt△ABD中,AB'=![]() BD=DB',
BD=DB',
又∵∠ADB=60°,
∴△ADB'是等边三角形,
∴AD=AB',
∴四边形AB'C'D是菱形;
(2)由平移可得,AB=C'D',∠ABD'=∠C'D'B=30°,
∴AB∥C'D',
∴四边形ABC'D'是平行四边形,
由(1)可得,AC'⊥B'D,
∴四边形ABC'D'是菱形,
∵AB=![]() AD=
AD=![]() ,
,
∴四边形ABC'D′的周长为4![]() ,
,
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形如下:
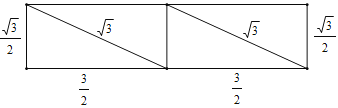
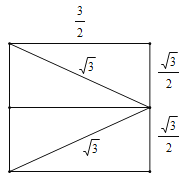
∴矩形周长为6+![]() 或2
或2![]() +3.
+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,有点(﹣2,a+3),B(b,b﹣3).
(1)当点A在第二象限的角平分线上时,求a的值;
(2)当点B到x轴的距离是它到y轴的距离2倍时,求点B所在的象限位置. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算x34x2的结果是( )
A.4x5
B.5x6
C.4x6
D.5x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间房.求该店有客房多少间?房客多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点
 出发,在矩形
出发,在矩形 边上沿着
边上沿着 的方向匀速移动,到达点
的方向匀速移动,到达点 时停止移动.已知机器人的速度为
时停止移动.已知机器人的速度为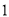 个单位长度/
个单位长度/ ,移动至拐角处调整方向需要
,移动至拐角处调整方向需要
 (即在
(即在 、
、 处拐弯时分别用时
处拐弯时分别用时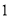
 ).设机器人所用时间为
).设机器人所用时间为 时,其所在位置用点
时,其所在位置用点 表示,
表示, 到对角线
到对角线 的距离(即垂线段
的距离(即垂线段 的长)为
的长)为 个单位长度,其中
个单位长度,其中 与
与 的函数图像如图②所示.
的函数图像如图②所示.(1)求
 、
、 的长;
的长;(2)如图②,点
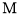 、
、 分别在线段
分别在线段 、
、 上,线段
上,线段 平行于横轴,
平行于横轴,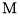 、
、 的横坐标分别为
的横坐标分别为 、
、 .设机器人用了
.设机器人用了 到达点
到达点 处,用了
处,用了 到达点
到达点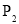 处(见图①).若
处(见图①).若 ,求
,求 、
、 的值.
的值.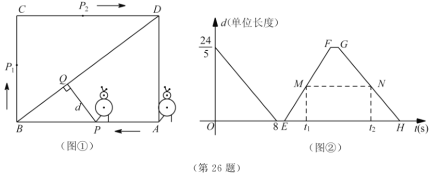
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国的数学研究具有悠久的历史,《九章算术》是我国的一部古典数学名著,但对其成书的年代说法不一,一般认为在公元前后,距今约2 000年.将2 000用科学记数法表示为( )
A.2×103
B.2×104
C.20×103
D.0.2×103 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数
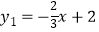 与x轴、y轴分别相交于点A和点B,直线
与x轴、y轴分别相交于点A和点B,直线 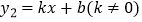 经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.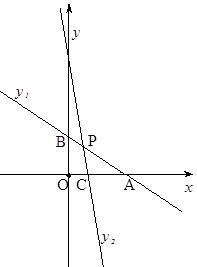
(1)求△ABO的面积;
(2)若△ABO被直线CP分成的两部分的面积相等,求点P的坐标及直线CP的函数表达式。
相关试题

