【题目】如图,点E在线段CD上,AE,BE分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x-3)2+|y-4|=0.
(1)求AD和BC的长;
(2)你认为AD和BC有怎样的位置关系?并说明理由.

参考答案:
【答案】(1) AD=3,BC=4;(2)AD∥BC.理由见解析.
【解析】
(1)根据题意可知x-3=0,y-4=0,易求解AD和BC的长;(2)根据∠AEB=90°,可得∠EAB+∠EBA=90°,因为EA、EB分别平分∠DAB和∠CBA,则∠DAB+∠ABC=180°,所以AD∥BC.
(1)∵(x-3)2+|y-4|=0,
∴x-3=0,y-4=0,解得x=3,y=4.
∴AD=3,BC=4.
(2)AD∥BC.
理由:∵AE,BE分别平分∠DAB和∠CBA,
∴∠DAE=∠EAB,∠CBE=∠EBA.
∵∠AEB=90°,
∴∠EAB+∠EBA=90°,
∴∠DAE+∠CBE=90°,
∴∠EAB+∠EBA+∠DAE+∠CBE=180°,
即∠DAB+∠CBA=180°,∴AD∥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )
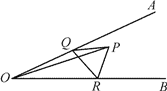
A. 6 B. 12 C. 16 D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一边长为40cm的正方形硬纸板,进行适当的剪裁,折成一个长方形盒子(纸板的厚度忽略不计).
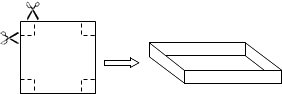
(1)如图,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方形盒子. ①要使折成的长方形盒子的底面积为484cm2 , 那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方形盒子,若折成的一个长方形盒子的表面积为550cm2 , 求此时长方形盒子的长、宽、高(只需求出符合要求的一种情况). -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:
(x﹣1)(x+1)=x2﹣1;(x﹣1)(x2+x+1)=x3﹣1;(x﹣1)(x3+x2+x+1)=x4﹣1.
根据各式的规律,可推测:(x﹣1)(xn﹣1+xn﹣2+…+x+1)=_____.
根据你的结论计算:1+3+32+33+…+32013+32014的个位数字是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线 y=
 x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).(1)当 x =______________时,PB+PC 的值最小;
(2)当 x =______________时,|PB-PC|的值最大.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2﹣4x﹣2经过A,B两点.
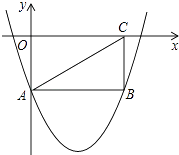
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿AO,OC,CB边向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒.
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,∠HOQ>∠POQ,求点H的纵坐标的取值范围.
相关试题

