【题目】如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm,求平行四边形ABCD的周长.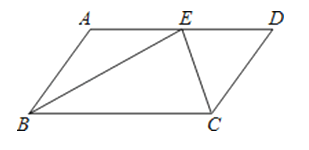
参考答案:
【答案】解:在平行四边形ABCD中,
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABE=∠EBC,∠BCE=∠ECD.,
∴∠EBC+∠BCE=90°,
∴∠BEC=90°,
∴BC2=BE2+CE2=122+52=132
∴BC=13cm,
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠AEB=∠ABE,
∴AB=AE,
同理CD=ED,
∵AB=CD,
∴AB=AE=CD=ED=![]() BC=6.5cm,
BC=6.5cm,
∴平行四边形ABCD的周长=2(AB+BC)=2(6.5+13)=39cm
【解析】根据角平分线的定义和平行线的性质得到等腰三角形ABE和等腰三角形CDE和直角三角形BCE.根据直角三角形的勾股定理得到BC=13.根据等腰三角形的性质得到AB.CD,从而求得该平行四边形的周长.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-1,2)关于x轴对称的点的坐标是( )
A. (-1,2)B. (-2,1)C. (-1,-2)D. (1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的折线图描述了某地某日的气温变化情况.根据图中信息,下列说法错误的是( )

A.4:00气温最低,14:00气温最高
B.12:00气温为30℃
C.这一天温差为9℃
D.气温是24℃的为6:00和8:00 -
科目: 来源: 题型:
查看答案和解析>>【题目】某果园2017年水果产量为100吨,2019年水果产量为196吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为( )
A. 196(1﹣x)2B. 100(1﹣x)2=196;C. 196(1+x)2=100;D. 100(1+x)2=196
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣12x+27=0的两个根是等腰三角形的底和腰,则这个三角形的周长为( )
A.21
B.21或15
C.15
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形的直角边分别为5和12,则斜边上的中线为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )

A.24 B.12 C.6 D.3
相关试题

