【题目】抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
①abc>0;
②a+b>0;
③若点A(﹣3,y1),点B(3,y2)都在抛物线上,则y1<y2;
④a(m﹣1)+b=0;
⑤若c≤﹣1,则b2﹣4ac≤4a.
其中结论错误的是 .(只填写序号)
参考答案:
【答案】③⑤
【解析】
试题分析:根据题意画出抛物线的大致图象,利用函数图象,由抛物线开口方向得a>0,由抛物线的对称轴位置得b<0,由抛物线与y轴的交点位置得c<0,于是可对①进行判断;由于抛物线过点(﹣1,0)和(m,0),且1<m<2,根据抛物线的对称性和对称轴方程得到0<﹣![]() <
<![]() ,变形可得a+b>0,则可对②进行判断;利用点A(﹣3,y1)和点B(3,y2)到对称轴的距离的大小可对③进行判断;根据抛物线上点的坐标特征得a﹣b+c=0,am2+bm+c=0,两式相减得am2﹣a+bm+b=0,然后把等式左边分解后即可得到a(m﹣1)+b=0,则可对④进行判断;根据顶点的纵坐标公式和抛物线对称轴的位置得到
,变形可得a+b>0,则可对②进行判断;利用点A(﹣3,y1)和点B(3,y2)到对称轴的距离的大小可对③进行判断;根据抛物线上点的坐标特征得a﹣b+c=0,am2+bm+c=0,两式相减得am2﹣a+bm+b=0,然后把等式左边分解后即可得到a(m﹣1)+b=0,则可对④进行判断;根据顶点的纵坐标公式和抛物线对称轴的位置得到![]() <c≤﹣1,变形得到b2﹣4ac>4a,则可对⑤进行判断.
<c≤﹣1,变形得到b2﹣4ac>4a,则可对⑤进行判断.
解:如图,
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以①的结论正确;
∵抛物线过点(﹣1,0)和(m,0),且1<m<2,
∴0<﹣![]() <
<![]() ,
,
∴![]() +
+![]() =
=![]() >0,∴a+b>0,所以②的结论正确;
>0,∴a+b>0,所以②的结论正确;
∵点A(﹣3,y1)到对称轴的距离比点B(3,y2)到对称轴的距离远,
∴y1>y2,所以③的结论错误;
∵抛物线过点(﹣1,0),(m,0),
∴a﹣b+c=0,am2+bm+c=0,
∴am2﹣a+bm+b=0,
a(m+1)(m﹣1)+b(m+1)=0,
∴a(m﹣1)+b=0,所以④的结论正确;
∵![]() <c,
<c,
而c≤﹣1,
∴![]() <﹣1,
<﹣1,
∴b2﹣4ac>4a,所以⑤的结论错误.
故答案为③⑤.
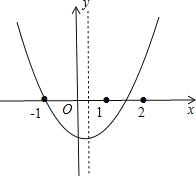
-
科目: 来源: 题型:
查看答案和解析>>【题目】“两直线平行,同旁内角互补”的逆命题为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的三边长a,b,c满足(a+c)(a-c)=b2,则该三角形是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 都有可能
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强的年龄比妈妈小33岁,今年妈妈的年龄正好是小强的4倍,小强今年的年龄是
A. 10岁 B. 11岁 C. 12岁 D. 13岁
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=
 (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )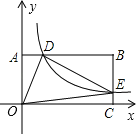
A.
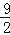 B.
B. C.
C. D.12
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】属于同类项的一组是
A. -3x2y与4xy2 B. 2x2y与-x2z
C. 4mn与-4nm D. -0.5ab与abc
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的标价为120元,若以九折降价出售,相对于进价仍获利20%,则该商品的进价是
A. 95元 B. 90元 C. 85元 D. 80元
相关试题

