【题目】如图,点O是边长为4 ![]() 的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1 , B1C1交BC于点D,B1C1交AC于点E,则DE= .
的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1 , B1C1交BC于点D,B1C1交AC于点E,则DE= . 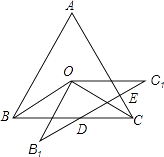
参考答案:
【答案】6﹣2 ![]()
【解析】解:令OB1与BC的交点为F,B1C1与AC的交点为M,过点F作FN⊥OB于点N,如图所示. 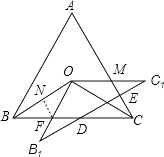
∵将△OBC绕点O逆时针旋转30°得到△OB1C1 ,
∴∠BOF=30°,
∵点O是边长为4 ![]() 的等边△ABC的内心,
的等边△ABC的内心,
∴∠OBF=30°,OB= ![]() AB=4,
AB=4,
∴△FOB为等腰三角形,BN= ![]() OB=2,
OB=2,
∴BF= ![]() =
= ![]() =OF.
=OF.
∵∠OBF=∠OB1D,∠BFO=∠B1FD,
∴△BFO∽△B1FD,
∴ ![]() .
.
∵B1F=OB1﹣OF=4﹣ ![]() ,
,
∴B1D=4 ![]() ﹣4.
﹣4.
在△BFO和△CMO中,有 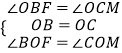 ,
,
∴△BFO≌△CMO(ASA),
∴OM=BF= ![]() ,C1M=4﹣
,C1M=4﹣ ![]() ,
,
在△C1ME中,∠C1ME=∠MOC+∠MCO=60°,∠C1=30°,
∴∠C1EM=90°,
∴C1E=C1Msin∠C1ME=(4﹣ ![]() )×
)× ![]() =2
=2 ![]() ﹣2.
﹣2.
∴DE=B1C1﹣B1D﹣C1E=4 ![]() ﹣(4
﹣(4 ![]() ﹣4)﹣(2
﹣4)﹣(2 ![]() ﹣2)=6﹣2
﹣2)=6﹣2 ![]() .
.
所以答案是:6﹣2 ![]() .
.
【考点精析】通过灵活运用等边三角形的性质和三角形的内切圆与内心,掌握等边三角形的三个角都相等并且每个角都是60°;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①是棱长为a的小正方体,如图②、如图③是由若干这样相同的小正方体摆放而成,按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层中小正方体的个数为s(提示:第一层中,s=1;第二层中,s=3),则第n层中,s=________.(用含n的式子表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
(2)如果MN=6 cm,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(π﹣3.14)0﹣|
 sin60°﹣4|+(
sin60°﹣4|+(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
(1)①若m=50,则射线OC的方向是________;
②图中与∠BOE互余的角有__________,与∠BOE互补的角有__________.
(2)若射线OA是∠BON的平分线,则∠BOS与∠AOC是否存在确定的数量关系?如果存在,请写出你的结论以及计算过程;如果不存在,请说明理由.

相关试题

