【题目】某校八年级数学兴趣小组的同学调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图。依据图中信息,解答下列问题:


(1)接受这次调查的家长共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,“很赞同”的家长占被调查家长总数的百分比是 ;
(4)在扇形统计图中,“不赞同”的家长部分所对应扇形的圆心角度数是 度.
(5)请同学们对“初中生带手机上学”现象说说你的看法.
参考答案:
【答案】(1)200;(2)见解析;(3) 10%;(4)162 ;(5)见解析.
【解析】试题分析:(1)根据赞同的人数和所占的百分比即可求出总人数;
(2)根据(1)求出无所谓的人数可直接画出条形统计图;
(3)用总人数减去其它的人数求出很赞同的人数,用很赞同的人数和总人数相比即可求出其所占百分比;
(4)用不赞同人数所除以总人数再乘以360°求出“不赞同”的家长部分所对应扇形的圆心角度数;
(5)根据学生现在正需要好好地学习,不应该带手机,网络这么发达,会影响学习.
试题解析:(1)本次调查的学生家长有50÷25%=200(名),
故答案为:200;
(2)无所谓的人数是:200×20%=40(人),
见下图黑色部分为所补部分:

(3)20÷200×100%=10%,
故答案为:10%;
(4)90÷200×360°=162°,
故答案为:162°;
(5)若学生回答合情合理即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如右图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.

(1)请在图中画出平移后的△ABC
(2)再在图中画出△ABC的高CD
(3)
 =
= (4)在右图中能使
 的格点P的个数有 个(点P异于A) .
的格点P的个数有 个(点P异于A) . -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项式乘方(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)64的展开式中第三项的系数为( )
A. 2016 B. 2017 C. 2018 D. 2019
-
科目: 来源: 题型:
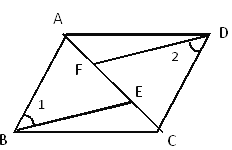
查看答案和解析>>【题目】如图,已知A,F,E,C在同一直线上,AB∥CD,∠1=∠2,AF=CE.
(1)写出图中全等的三角形;
(2)选择其中一对,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店用1000元人民币购进水果销售,过了一段时间,又用2400元人民币购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的贵了2元.
(1)该商店第一次购进水果多少千克?
(2)假设该商店两次购进的水果按相同的标价销售,最后剩下的20千克按标价的五折优惠销售.若两次购进水果全部售完,利润不低于950元,则每千克水果的标价至少是多少元?
注:每千克水果的销售利润等于每千克水果的销售价格与每千克水果的购进价格的差,两批水果全部售完的利润等于两次购进水果的销售利润之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数字9 600 000用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
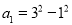 ,
, 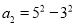 ,……,
,……, 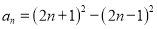 ,(n为正整数)
,(n为正整数)(1)试说明
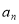 是8的倍数;
是8的倍数;(2)若△ABC的三条边长分别为
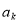 、
、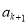 、
、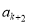 (
(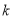 为正整数)
为正整数)①求
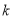 的取值范围.
的取值范围.②是否存在这样的
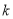 ,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
相关试题

