搜索
【题目】解方程：(x－1)(1＋x)－(x＋2)(x－3)＝2x－5.
参考答案：
【答案】x＝10
【解析】试题分析：根据平方差公式和多项式乘多项式法则去括号后合并同类项即可得关于x的一元一次方程，解之可得．
试题解析：去括号，得x＋x2－1－x－x2＋3x－2x＋6＝2x－5，
移项、合并同类项，得－x＋10＝0，
解得x＝10.
-
科目： 来源： 题型：
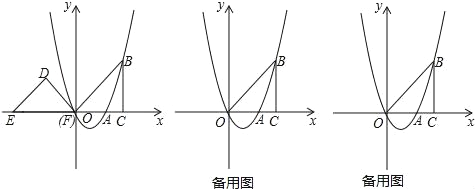
查看答案和解析>>【题目】如图，抛物线y=ax2+bx（a≠0）经过点A（2，0），点B（3，3），BC⊥x轴于点C，连接OB，等腰直角三角形DEF的斜边EF在x轴上，点E的坐标为（-4，0），点F与原点重合
（1）求抛物线的解析式并直接写出它的对称轴；
（2）△DEF以每秒1个单位长度的速度沿x轴正方向移动，运动时间为t秒，当点D落在BC边上时停止运动，设△DEF与△OBC的重叠部分的面积为S，求出S关于t的函数关系式；
（3）点P是抛物线对称轴上一点，当△ABP是直角三角形时，请直接写出所有符合条件的点P坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．
性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．
理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．
应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O．
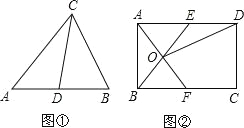
（1）求证：△AOB和△AOE是“友好三角形”；
（2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．
探究：在△ABC中，∠A=30°，AB=4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的
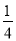，请直接写出△ABC的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成续时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分与9个原始评分相比，不变的数字特征是（ ）
A. 平均数B. 中位数C. 众数D. 方差
-
科目： 来源： 题型：
查看答案和解析>>【题目】望江中学为了了解学生平均每天“诵读经典”的时间，在全校范围内随机抽查了部分学生进行调查统计，并将调查统计的结果分为：每天诵读时间t≤20分钟的学生记为A类，20分钟＜t≤40分钟的学生记为B类，40分钟＜t≤60分钟的学生记为C类，t＞60分钟的学生记为D类四种．将收集的数据绘制成如下两幅不完整的统计图．请根据图中提供的信息，解答下列问题：
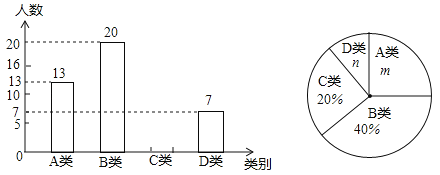
（1）m=%，n=%，这次共抽查了名学生进行调查统计；
（2）请补全上面的条形统计图；
（3）如果该校共有1200名学生，请你估计该校C类学生约有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直角梯形OABC中，AB∥OC，点A坐标为（0，6），点C坐标为（3，0），BC=
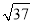，一抛物线过点A、B、C．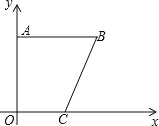
（1）填空：点B的坐标为 ；
（2）求该抛物线的解析式；
（3）作平行于x轴的直线与x轴上方的抛物线交于点E、F，以EF为直径的圆恰好与x轴相切，求该圆的半径．
-
科目： 来源： 题型：
查看答案和解析>>【题目】组成多项式2x2﹣x﹣3的单项式是下列几组中的（ ）
A. 2x2，x，3 B. 2x2，﹣x，﹣3 C. 2x2，x，﹣3 D. 2x2，﹣x，3
相关试题
