【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.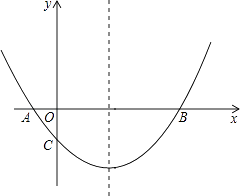
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:设抛物线的解析式为y=ax2+bx+c(a≠0),
∵A(﹣1,0),B(5,0),C(0,- ![]() )三点在抛物线上,
)三点在抛物线上,
∴  ,
,
解得 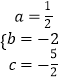 .
.
∴抛物线的解析式为:y= ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() ;
;
(2)
解:∵抛物线的解析式为:y= ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() ,
,
∴其对称轴为直线x=﹣ ![]() =﹣
=﹣ ![]() =2,
=2,
连接BC,如图1所示,
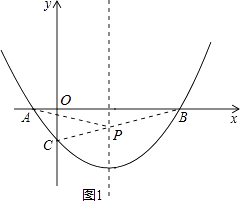
∵B(5,0),C(0,﹣ ![]() ),
),
∴设直线BC的解析式为y=kx+b(k≠0),
∴ 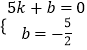 ,
,
解得 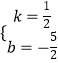 ,
,
∴直线BC的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
当x=2时,y=1﹣ ![]() =﹣
=﹣ ![]() ,
,
∴P(2,﹣ ![]() );
);
(3)
解:存在.
如图2所示,
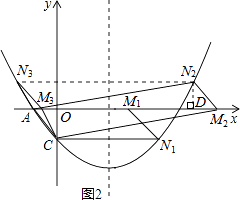
①当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C(0,﹣ ![]() ),
),
∴N1(4,﹣ ![]() );
);
②当点N在x轴上方时,
如图,过点N2作N2D⊥x轴于点D,
在△AN2D与△M2CO中,
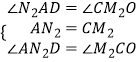
∴△AN2D≌△M2CO(ASA),
∴N2D=OC= ![]() ,即N2点的纵坐标为
,即N2点的纵坐标为 ![]() .
.
∴ ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() =
= ![]() ,
,
解得x=2+ ![]() 或x=2﹣
或x=2﹣ ![]() ,
,
∴N2(2+ ![]() ,
, ![]() ),N3(2﹣
),N3(2﹣ ![]() ,
, ![]() ).
).
综上所述,符合条件的点N的坐标为(4,﹣ ![]() ),(2+
),(2+ ![]() ,
, ![]() )或(2﹣
)或(2﹣ ![]() ,
, ![]() ).
).
【解析】本题考查的是二次函数综合题,涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识,在解答(3)时要注意进行分类讨论.(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(﹣1,0),B(5,0),C(0,- ![]() )三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
)三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
【考点精析】本题主要考查了确定一次函数的表达式和平行四边形的判定与性质的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】佳佳果品店在批发市场购买某种水果销售,第一次用1 200元购进若干千克,并以8元/kg出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1 452元所购买的数量比第一次多20 kg,以9元/kg售出100 kg后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,
, ,
, ,
, ,把一条长为2016个单位长度且没有弹性的细线
,把一条长为2016个单位长度且没有弹性的细线 线的粗细忽略不计
线的粗细忽略不计 的一端固定在点A处,并按
的一端固定在点A处,并按 的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是
的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是


A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学同时从山脚开始爬山,到达山顶后立即下山,在山脚和山顶之间不断往返运动,已知山坡长为360m,甲、乙上山的速度比是6:4,并且甲、乙下山的速度都是各自上山速度的1.5倍,当甲第三次到达山顶时,则此时乙所在的位置是
 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目
学生数(名)
百分比
丢沙包
20
10%
打篮球
60
p%
跳大绳
n
40%
踢毽球
40
20%
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;

(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
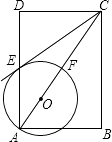
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=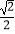 ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
相关试题

