【题目】如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(﹣3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.

(1)求点C的坐标和直线l1的解析式;
(2)若将点C先向左平移3个单位长度,再向上平移6个单位长度得到点D,请你判断点D是否在直线l1上;
(3)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
参考答案:
【答案】(1)直线l1的解析式为y=﹣2x﹣3;(2)点D在直线l1上;(3)13.5.
【解析】
试题分析:(1)根据平移的性质得到点C的坐标;把点B、C的坐标代入直线方程y=kx+b(k≠0)来求该直线方程;
(2)根据平移的性质得到点D的坐标,然后将其代入(1)中的函数解析式进行验证即可;
(3)根据点B的坐标求得直线l2的解析式,据此求得相关线段的长度,并利用三角形的面积公式进行解答.
解:(1)∵B(﹣3,3),将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,
∴﹣3+1=﹣2,3﹣2=1,
∴C的坐标为(﹣2,1),
设直线l1的解析式为y=kx+c,
∵点B、C在直线l1上,
∴代入得:![]()
解得:k=﹣2,c=﹣3,
∴直线l1的解析式为y=﹣2x﹣3;
(2)∵将点C先向左平移3个单位长度,再向上平移6个单位长度得到点D,C(﹣2,1),
∴﹣2﹣3=﹣5,1+6=7,
∴D的坐标为(﹣5,7),
代入y=﹣2x﹣3时,左边=右边,
即点D在直线l1上;
(3)把B的坐标代入y=x+b得:3=﹣3+b,
解得:b=6,
∴y=x+6,
∴E的坐标为(0,6),
∵直线y=﹣2x﹣3与y轴交于A点,
∴A的坐标为(0,﹣3),
∴AE=6+3=9,
∵B(﹣3,3),
∴△ABE的面积为![]() ×9×|﹣3|=13.5.
×9×|﹣3|=13.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式x2﹣3x+2的值为6,则多项式3x2﹣9x﹣5的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球与太阳的平均距离大约为150 000 000km,用科学记数法表示__________km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆轿车从甲地驶往乙地,到达乙地后返回甲地,速度是原来的1.5倍,共用t小时.设轿车行驶的时间为x(h),轿车到甲地的距离为y(km),轿车行驶过程中y与x之间的函数图象如图.
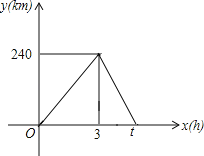
(1)求轿车从乙地返回甲地时的速度和t的值;
(2)求轿车从乙地返回甲地时y与x之间的函数关系式,并写出自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图所示,小明准备在C处牵牛到河边AB饮水,按下列要求作图并说明理由.
①请用三角板作出小明的最短路线(不考虑其他因素);
②如图乙,若小明在C处牵牛到河边AB饮水,并且必须到河边D处观察河水的水质情况,请作出小明行走的最短路线。

(2)经过平移,图中左边图形上A点移到E点,作出平移后的图形。

理由: ;理由: 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式A与多项式B的和是3x+x2,多项式B与多项式C的和是﹣x+3x2,那么多项式A减去多项式C的差是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程( )
A. 54﹣x=20%×108 B. 54﹣x=20%(108+x)
C. 54+x=20%×162 D. 108﹣x=20%(54+x)
相关试题

