【题目】如图,在△ABC中,AB=BC,∠ABC=90°,点F为AB延长线上一点,点E在BC上,BE=BF,连接AE,EF和CF.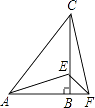
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠EFC的度数.
参考答案:
【答案】
(1)证明:∵∠ABC=90°,F为AB延长线上一点,
∴∠ABC=∠CBF=90°.
在△ABE和△CBF中,
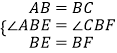 ,
,
∴△ABE≌△CBF
(2)解:∵在△ABC中,AB=BC,∠ABC=90°,点F为AB延长线上一点,点E在BC上,BE=BF,
∴△ABC和△EBF都是等腰直角三角形,
∴∠ACB=∠EFB=45°.
∵∠CAE=30°,
∴∠AEB=∠CAE+∠ACB=30°+45°=75°.
由(1)知△ABE≌△CBF,
∴∠CFB=∠AEB=75°.
∴∠EFC=∠CFB﹣∠EFB=75°﹣45°=30°
【解析】(1)根据已知条件由SAS得到△ABE≌△CBF;(2)由已知可得△ABC和△EBF都是等腰直角三角形,再根据由(1)知△ABE≌△CBF,求出∠EFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
-
科目: 来源: 题型:
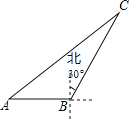
查看答案和解析>>【题目】如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程3xa﹣2﹣7=0是一个一元一次方程,则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】用平面去截五棱柱,在所得的截面中,不可能出现的是( )
A.八边形
B.四边形
C.六边形
D.三角形 -
科目: 来源: 题型:
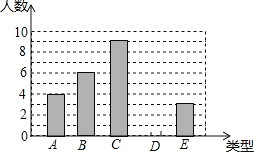
查看答案和解析>>【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
相关试题

