【题目】如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( ) 
A.4.5米
B.6米
C.7.2米
D.8米
参考答案:
【答案】B
【解析】解:∵MC∥AB, ∴△DCM∽△DAB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ①,
①,
∵NE∥AB,
∴△FNE∽△FAB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ②,
②,
∴ ![]() =
= ![]() ,解得BC=3,
,解得BC=3,
∴ ![]() =
= ![]() ,解得AB=6,
,解得AB=6,
即路灯A的高度AB为6m.
故选B.
由MC∥AB可判断△DCM∽△DAB,根据相似三角形的性质得 ![]() =
= ![]() ,同理可得
,同理可得 ![]() =
= ![]() ,然后解关于AB和BC的方程组即可得到AB的长.
,然后解关于AB和BC的方程组即可得到AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给定直线l:y=kx,抛物线C:y=ax2+bx+1.

(1)当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线l′,则无论非零实数k取何值,直线l′与抛物线C都只有一个交点.
①求此抛物线的解析式;
②若P是此抛物线上任一点,过P作PQ∥y轴且与直线y=2交于Q点,O为原点.求证:OP=PQ. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点D、E分别在△ABC的边AB、AC上,下列给出的条件中,不能判定DE∥BC的是( )
A.BD:AB=CE:AC
B.DE:BC=AB:AD
C.AB:AC=AD:AE
D.AD:DB=AE:EC -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角△ABC中,∠C=90°,∠A、∠B与∠C的对边分别是a、b和c,那么下列关系中,正确的是( )
A.cosA=
B.tanA=
C.sinA=
D.cosA=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E在BC边上,且CE:BC=2:3,AC与DE相交于点F,若S△AFD=9,则S△EFC= .
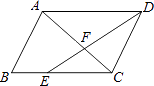
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,AB=DC,点P是AD边上一点,联结PB、PC,且AB2=APPD,则图中有对相似三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果
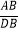 =m,
=m, 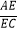 =n.那么m与n满足的关系式是:m=(用含n的代数式表示m).
=n.那么m与n满足的关系式是:m=(用含n的代数式表示m). 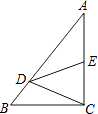
相关试题

