Question

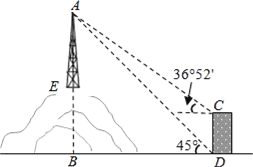
【题目】如图所示，某教学活动小组选定测量山顶铁塔AE的高，他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°，在楼顶C测得塔顶A的仰角为36°52′．若小山高BE=62m，楼的底部D与山脚在同一水平面上，求铁塔的高AE．（参考数据：sin36°52′≈0.60，tan36°52′≈0.75）

Answer 1

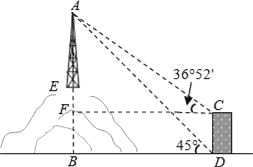
【答案】该铁塔的高AE为58米．

【解析】试题分析：根据楼高和山高可求出EF，继而得出AF，在Rt△AFC中表示出CF，在Rt△ABD中表示出BD，根据CF=BD可建立方程，解出即可．

试题解析：如图，过点C作CF⊥AB于点F．

设塔高AE=x，作CF⊥AB于点F，

则四边形BDCF是矩形，

∴CD=BF=30m，CF=BD，

∵在Rt△ADB中，∠ADB=45°，

∴AB=BD=x+62，

∵在Rt△ACF中，∠ACF=36°52′，CF=BD=x+62，AF=x+62﹣30=x+32，

∴tan36°52′=≈0.75，

∴x=58．

答：该铁塔的高AE为58米．