Question

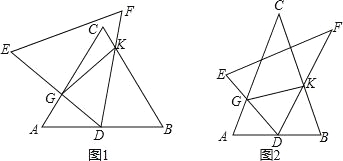
【题目】如图1，两个全等的等边三角形如图放置，边长为4，AC与DE交于点G，点D是AB的中点，BC与DF相交于点K，连接GK．

（1）写出两对相似三角形（不含全等）；

（2）求证：∠GKD=∠BKD；

（3）若△DKG的面积为S，KG=x，写出S与x的关系，并写出x的取值范围；

（4）若将条件中的两个全等的等边三角形改为两个全等的等腰三角形（DF=EF=AC=BC），如图2，其余条件不变，直接判断（1）（2）中的结论是否依然成立．

Answer 1

【答案】（1）△DAG∽△KBD，△KDG∽△KDB；（2）证明参见解析；（3）S=x（2≤x≤3）；（4）结论依然成立；

【解析】

试题分析：（1）由等边三角形的性质得出∠A=∠B=∠EDF=60°，再由三角形的外角性质得出∠AGD=∠BDK，利用两角相等证出△DAG∽△KBD，从而得出对应边成比例，又由题意可得AD=BD=2，得出，根据两边对应成比例，夹角相等证出△KDG∽△KDB即可；（2）由等边三角形的性质得出∠A=∠B=∠EDF=60°，再由三角形的外角性质得出∠AGD=∠BDK，证出△DAG∽△KBD，得出对应边成比例，由AD=BD=2，得出，证出△KDG∽△KDB，即可得出结论；（3）由等腰三角形的性质得出∠A=∠B=∠EDF，再由三角形的外角性质得出∠AGD=∠BDK，证出△DAG∽△KBD，得出对应边成比例，由AD=BD=2，得出，证出△KDG∽△KDB；从而得到△DAG∽△KDG，所以，即，得出DGDK=2x，△DKG的面积S=DGDKsin∠EDF，即可得出结果；当KG∥AB时，KG最小=AB=2；当K与C重合时，KG最大=3；即可得出x的取值范围；（4）结论仍然成立，解法同（1）（2），利用两角相等两个三角形相似证明△DAG∽△KBD，根据两边对应成比例，夹角相等两个三角形相似证出△KDG∽△KDB．

试题解析：（1）写出两对三角形可以是△DAG∽△KBD，△KDG∽△KDB；理由如下：∵△ABC和△DEF是两个全等的等边三角形，∴∠A=∠B=∠EDF=60°，∵∠BDG=∠A+∠AGD，∠BDG=∠BDK+∠EDF，∴∠AGD=∠BDK，∴△DAG∽△KBD，∴，∵点D是AB的中点，∴AD=BD=2，∴，∴△KDG∽△KDB；（2）证明：∵△ABC和△DEF是两个全等的等边三角形，∴∠A=∠B=∠EDF=60°，∵∠BDG=∠A+∠AGD，∠BDG=∠BDK+∠EDF，∴∠AGD=∠BDK，∴△DAG∽△KBD，∴，∵点D是AB的中点，∴AD=BD=2，∴，又∵∠GDK=∠DBK，∴△KDG∽△KDB，∴∠GKD=∠BKD；（3）由（2）得：△DAG∽△KBD，△KDG∽△KDB，∴△DAG∽△KDG，∴，即，∴DGDK=2x，∴△DKG的面积S=DGDKsin∠EDF=2x=x，当KG∥AB时，KG最小=AB=2；当K与C重合时，KG最大=3；∴S=x（2≤x≤3）；（4）（1）（2）中的结论依然成立；理由如下：∵△ABC和△DEF是两个全等的等腰三角形，DF=EF=AC=BC，∴∠A=∠B=∠EDF，∵∠BDG=∠A+∠AGD，∠BDG=∠BDK+∠EDF，∴∠AGD=∠BDK，∴△DAG∽△KBD，∴，∵点D是AB的中点，∴AD=BD=2，∴，又∵∠GDK=∠DBK，∴△KDG∽△KDB，∴∠GKD=∠BKD．