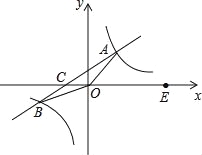
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象相交于A,B两点,直线AB与x轴相交于点C,点B的坐标为(﹣6,m),线段OA=5,E为x轴正半轴上一点,且cos∠AOE=
的图象相交于A,B两点,直线AB与x轴相交于点C,点B的坐标为(﹣6,m),线段OA=5,E为x轴正半轴上一点,且cos∠AOE=![]() .
.
(1)求反比例函数的解析式;
(2)求证:S△AOC=2S△BOC;
(3)直接写出当y1>y2时,x的取值范围.
参考答案:
【答案】(1)反比例函数解析式为![]() ;
;
(2)证明见解析
(3)当y1>y2时,x的取值范围为﹣6<x<0或x>3.

【解析】
试题分析:(1)通过解直角三角形求出点A的坐标,进而得出反比例函数解析式;
(2)先根据反比例函数解析式求得点B的坐标,再由点A、B的坐标利用待定系数法求出直线AB的解析式,进而得到OC的长,最后计算△AOC和△BOC的面积并得出结论;
(3)结合两函数图象,找出反比例函数图象在一次函数图象下方时x的取值范围即可.
试题解析:过点A作AD⊥x轴于点D,∵cos∠AOE=![]() =
=![]() ,∴OD=3
,∴OD=3
∴AD=![]() =4,∴A(3,4),将点A的坐标代入反比例函数y2=
=4,∴A(3,4),将点A的坐标代入反比例函数y2=![]() 得,a=12
得,a=12
∴反比例函数解析式为![]() ;
;
(2)将点B(﹣6,m)代入反比例函数![]() 得,m=﹣2,∴B(﹣6,﹣2)
得,m=﹣2,∴B(﹣6,﹣2)
将A(3,4),B(﹣6,m)代入一次函数y1=kx+b,得
![]() ,解得
,解得![]()
∴一次函数解析式为![]()
当y=0时,![]() ,即x=﹣3,∴C(﹣3,0),∴OC=3
,即x=﹣3,∴C(﹣3,0),∴OC=3
∴△AOC的面积=![]() ×3×4=6
×3×4=6
△BOC的面积=![]() ×3×2=3
×3×2=3
∴S△AOC=2S△BOC;
(3)当y1>y2时,x的取值范围为﹣6<x<0或x>3.

-
科目: 来源: 题型:
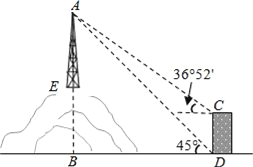
查看答案和解析>>【题目】如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角为36°52′.若小山高BE=62m,楼的底部D与山脚在同一水平面上,求铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=(m+2)x+1,函数y的值随x值的增大而增大,则m的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列选项中的三条线段能组成三角形的是( )
A. 2,2,6 B. 1,2,3 C. 4,5,6 D. 8,3,2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知P(3,3),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种细胞的直径是0.00000085米,将其用科学记数法表示为 ( )
A. 8.5×10-8B. 8.5×10-7C. 0.85×10-7D. 85×10-8
-
科目: 来源: 题型:
查看答案和解析>>【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别
消费额(元)
A
10≤x<100
B
100≤x<200
C
20≤x<300
D
300≤x<400
E
x≥400
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?

相关试题

