搜索
【题目】一个等腰三角形的底边长为5，一腰上的中线把它的周长分成的两部分的差为2，则这个等腰三角形的腰长为________．
参考答案：
【答案】3或7
【解析】
设腰长为2x，根据题意可得方程（2x+x）-（5+x）=2或（5+x）-（2x+x）=2，解方程求得x值后，再根据三角形三边关系进行验证即可
设腰长为2x，根据一腰上的中线把它的周长分成的两部分的差为2可得，
（2x+x）-（5+x）=2或（5+x）-（2x+x）=2，
解得：x=3.5，x=1.5，
∴2x=7或3，
①三角形ABC三边长为7、7、5，符合三角形三边关系定理；
②三角形ABC三边是3、3、5，符合三角形三边关系定理.
故答案为：3或7
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一个有40个数据的样本统计分成6组，若某一组的频率为0.15，则该组的频数约是（ ）
A.1
B.0.9
C.6.67
D.6 -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：|﹣3|+（﹣4）0=________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，CD是AB边上的中线，E是CD的中点，过点C作AB的平行线交AE的延长线于点F，连接BF．
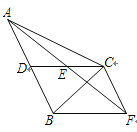
(1) 求证：CF＝AD；
(2) 若CA＝CB，∠ACB＝90°，试判断四边形CDBF的形状，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知函数 y=x+1 的图象与 y 轴交于点 A，一次函数 y=kx+b 的图象经过点 B（0，﹣1），与x 轴 以及 y=x+1 的图象分别交于点 C、D，且点 D 的坐标为（1，n），
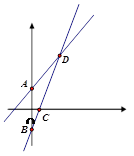
（1）则n= ，k= ，b= ；
（2）函数 y=kx+b 的函数值大于函数 y=x+1 的函数值，则X的取值范围是 ；
（3）求四边形 AOCD 的面积；
（4）在 x轴上是否存在点 P，使得以点 P，C，D 为顶点的三角形是直角三角形？若存在求出点 P 的坐标； 若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】对某班学生睡眠时间进行调查后，将所得的数据分成5组，第一组的频率是0.16，第二、三、四组的频率之和为0.64，则第五组的频率是（ ）
A.0.38
B.0.30
C.0.20
D.0.19 -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中， AB、BC、AC三边的长分别为
、 
、 
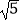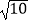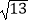，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．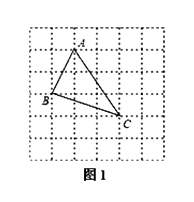
（1）△ABC的面积为： ．
（2）若△DEF三边的长分别为 、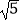 
、 
，请在图2的正方形网格中画出相应的△DEF，并利用构图法求出它的面积．
（3）如图3，一个六边形的花坛被分割成7个部分，其中正方形PRBA，RQDC，QPFE的面积分别为13、10、17，请利用第2小题解题方法求六边形花坛ABCDEF的面积．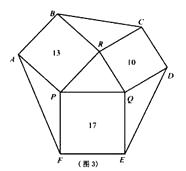
相关试题
