【题目】(1)如图①,在△ABC中,已知∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.请写出图中的等腰三角形,并找出EF与BE、CF间的关系;
(2) 如图②中∠ABC的平分线与三角形ABC的外角∠ACG的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.图中有等腰三角形吗?如果有,请写出来.EF与BE、CF间的关系如何?请说明理由.

参考答案:
【答案】(1)等腰三角形有△EBO和△CFO,EF=BE+CF;(2)有等腰三角形,它们分别是△EBO和△CFO.EF=BE-CF.理由见解析.
【解析】
(1)由EF∥BC可得∠EOB=∠OBC,由OB平分∠ABC可得∠EBO=∠OBC,由此得到∠EOB=∠EBO,然后即可证明△BEO是等腰三角形,同理可证:△CFO是等腰三角形;根据等腰三角形的性质求得OE=EB,OF=FC,从而证得EF=BE+FC;
(2)根据角平分线的定义以及平行线的性质进行角之间的等量代换,根据等边对等角,发现两个等腰三角形:△BOE和△COF,即可得出所求的结论.
(1)等腰三角形有△EBO和△CFO,EF=BE+CF.
(2)有等腰三角形,它们分别是△EBO和△CFO.
EF=BE-CF.
理由:∵BO平分∠ABC,
∴∠ABO=∠OBC.
∵OE∥BC,
∴∠EOB=∠OBC,
∴∠EOB=∠EBO,
∴BE=EO.
同理,CF=OF,
∵EO=EF+OF,
∴EF=EO-OF=BE-CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.

(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
-
科目: 来源: 题型:
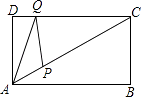
查看答案和解析>>【题目】如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.
(1)等腰直角三角形是不是“少见的三角形”?
(2)已知如图所示的钝角三角形是一个“少见的三角形”,请你画出分割线的大致位置,并求出顶角的度数;
(3)锐角三角形中有没有“少见的三角形”?如果没有,请说明理由;如果有,请画出图形并求出顶角的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).

(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1 , N关于BC的对称点为N2 , 求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答问题:当t为何值时,△PBQ是直角三角形?

相关试题

