【题目】如图,等边△ABC放置在平面直角坐标系中,已知A(0,0)、B(2,0),反比例函数的图象经过点C.
(1)求点C的坐标及反比例函数的解析式.
(2)如果将等边△ABC向上平移n个单位长度,使点B恰好落在双曲线上,求n的值.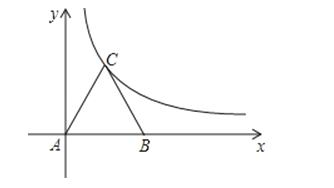
参考答案:
【答案】解:(1)过点C作CD⊥x轴,垂足为D,如图,设反比例函数的解析式为![]() ,
,
∵A(0,0)、B(2,0),
∴AB=2,
∵△ABC是等边三角形,
∴AC=AB=2,∠CAB=60°,
∴AD=1,CD=ACsin60=2×![]() =
=![]() ,
,
∴点C坐标为(1,![]() ),
),
∵反比例函数的图象经过点C,
∴k=1×![]() =
=![]() ,
,
∴反比例函数的解析式![]() ;
;
(2)∵将等边△ABC向上平移n个单位,则平移后B点坐标为(2,n),而平移后的点B恰好落在双曲线上,
∴2n=![]() ,
,
∴n=![]() .
.
【解析】(1)过点C作CD⊥x轴,垂足为D,如图,根据等边三角形的性质得到AC=AB=2,∠CAB=60°,AD=1,再利用三角函数可计算出CD![]() =
=![]() , 则点C坐标为(1,
, 则点C坐标为(1,![]() ),然后利用待定系数法求反比例函数解析式;
),然后利用待定系数法求反比例函数解析式;
(2)根据点平移规律得到平移后B点坐标为(2,n),然后根据反比例函数图象上点的坐标特征得到2n=![]() , 再解方程即可.
, 再解方程即可.
【考点精析】利用反比例函数的性质对题目进行判断即可得到答案,需要熟知性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】太阳与地球之间的平均距离约为150000000km,用科学记数法表示这一数据为( )
A.1.5×108 kmB.15×107 kmC.0.15×109 kmD.1.5×109 km
-
科目: 来源: 题型:
查看答案和解析>>【题目】)如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,E是线段AB上一点,过点E作x轴的垂线,交反比例函数图象于点F,若EF= AD,求出点E的坐标.
AD,求出点E的坐标.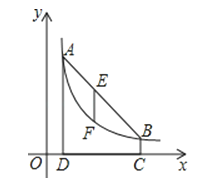
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:

如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点M(﹣2,1)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中为中心对称图形的是( )
A.等边三角形B.平行四边形C.抛物线D.五角星
相关试题

