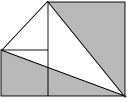
【题目】如图,在△ABC中,∠B=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线. 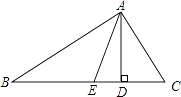
(1)求∠DAE的度数;
(2)写出以AD为高的所有三角形.
参考答案:
【答案】
(1)解:∵在△ABC中,AE是∠BAC的平分线,且∠B=40°,∠C=60°,
∴∠BAE=∠EAC= ![]() (180°﹣∠B﹣∠C)=
(180°﹣∠B﹣∠C)= ![]() (180°﹣40°﹣60°)=40°.
(180°﹣40°﹣60°)=40°.
在△ACD中,∠ADC=90°,∠C=60°,
∴∠DAC=180°﹣90°﹣60°=30°,
∠EAD=∠EAC﹣∠DAC=40°﹣30°=10°
(2)解:以AD为高的所有三角形:△ABC、△ABD、△ACE、△ABE、△ADF和△ACD
【解析】(1)根据三角形的内角和定理及角平分线的性质求解即可;(2)以AD为高的所有三角形是在BC线段上任意两点和点A组成的所有三角形.
【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内,以及对三角形的内角和外角的理解,了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
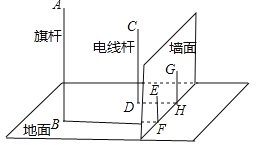
查看答案和解析>>【题目】如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
(1)请用直尺和圆规在图①中画一个以AB为边的“好玩三角形”;
(2)如图②,在Rt△ABC中,∠C=90°,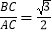 ,求证:△ABC是“好玩三角形”.
,求证:△ABC是“好玩三角形”. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
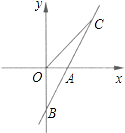
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某果园有100颗橙子树,平均每颗树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了x棵橙子树.
(1)直接写出平均每棵树结的橙子个数y(个)与x之间的关系;
(2)果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式(也称关系式);
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2的小正方形和边长为x的大正方形放在一起.
(1)用x表示阴影部分的面积;
(2)计算当x=5时,阴影部分的面积.
相关试题

