【题目】已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=1,连接DE,则DE= . 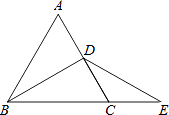
参考答案:
【答案】![]()
【解析】解:∵△ABC为等边三角形, ∴∠ABC=∠ACB=60°,AB=BC,
∵BD为中线,
∴∠DBC= ![]() ∠ABC=30°,
∠ABC=30°,
∵CD=CE,
∴∠E=∠CDE,
∵∠E+∠CDE=∠ACB,
∴∠E=30°=∠DBC,
∴BD=DE,
∵BD是AC中线,CD=1,
∴AD=DC=1,
∵△ABC是等边三角形,
∴BC=AC=1+1=2,BD⊥AC,
在Rt△BDC中,由勾股定理得:BD= ![]() =
= ![]() ,
,
即DE=BD= ![]() ,
,
故答案为: ![]() .
.
根据等腰三角形和三角形外角性质求出BD=DE,求出BC,在Rt△BDC中,由勾股定理求出BD即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在操场上活动时,小明发现旗杆的影子与旁边的树的影子好像平行,但他不敢确定,那么他可以采取的最好办法是( )
A. 通过平移的办法进行验证
B. 看看其他同学是不是这样认为
C. 构造并测量两个同位角,若相等则影子平行
D. 构造几何模型,用已学知识证明
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具专柜要经营一种新上市的儿童玩具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出专柜销售这种玩具,每天所得的销售利润W(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该玩具每天的销售利润最大;
(3)专柜结合上述情况,设计了A、B两种营销方案:
方案A:该玩具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件玩具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:矩形ABCD中,对角线AC与BD交于点O,∠BOC=120°,AC=4cm,求矩形ABCD的周长.
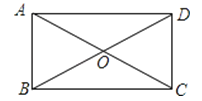
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,有一条小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,则这条小路的面积是m2 .
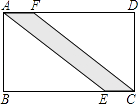
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的有( )
①垂直平分弦的直线经过圆心;②平分弦的直径一定垂直于弦;
③相等的圆周角所对的弧相等;④等弧所对的弦相等;
⑤等弦所对的弧相等.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,P是菱形ABCD的对角线AC上一动点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于x的函数图象的大致形状是( )
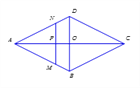
A.
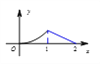 B.
B. 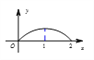 C.
C. 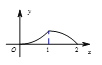 D.
D. 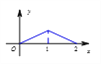
相关试题

