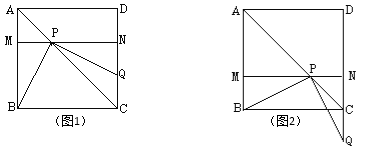
【题目】操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,设A、P两点间的距离为x.

探究:
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察到的结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应x的值;如果不可能,试说明理由.
参考答案:
【答案】(1)PQ=PB,证明过程见解析;(2)y=![]() (0≤x<
(0≤x<![]() );(3)x=0或1.
);(3)x=0或1.
【解析】
试题分析:(1)过点P作MN∥BC,分别交AB、CD于点M、N,则四边形AMND和四边形BCNM都是矩形,△AMP和△CNP都是等腰三角形,得出NP=NC=MB,从而证明△QNP≌△PMB,从而得出答案;(2)设AP=x,则M=MP=NQ=DN=![]() x,BM=PN=CN=1-
x,BM=PN=CN=1-![]() x,根据题意得出△PBC和△PCQ的面积,然后得出y与x的函数关系式;(3)本题分三种情况进行讨论,即①当点Q在边DC上;②当点Q在边DC的延长线上;③当点Q与C点重合.
x,根据题意得出△PBC和△PCQ的面积,然后得出y与x的函数关系式;(3)本题分三种情况进行讨论,即①当点Q在边DC上;②当点Q在边DC的延长线上;③当点Q与C点重合.
试题解析:(1)过点P作MN∥BC,分别交AB、CD于点M、N,则四边形AMND和四边形BCNM都是矩形,△AMP和△CNP都是等腰三角形(如图1),∴NP=NC=MB.
∵∠BPQ=90°∴∠QPN+∠BPM=90°,而∠BPM+∠PBM=90°∴∠QPN=∠PBM.
又∵∠QNP=∠PMB=90°∴△QNP≌△PMB(ASA),∴PQ=PB.
(2)由(1)知△QNP≌△PMB,得NQ=MP.
设AP=x,∴AM=MP=NQ=DN=![]() x,BM=PN=CN=1-
x,BM=PN=CN=1-![]() x
x
∴CQ=CD-DQ=1-2×![]() x=1-
x=1-![]() x
x
∴S△PBC=![]() BCBM=
BCBM=![]() ×1×(1-
×1×(1-![]() x)=
x)=![]() -
-![]() x,
x,
S△PCQ=![]() CQPN=
CQPN=![]() ×(1-
×(1-![]() x)(1-
x)(1-![]() x)=
x)=![]() ,
,
∴S四边形PBCQ=S△PBC+S△PCQ=![]() , 即y=
, 即y=![]() (0≤x<
(0≤x<![]() ).
).
(3)△PCQ可能成为等腰三角形.
①当点Q在边DC上,由![]() 得:
得:![]()
解得x1=0,x2=![]() (舍去);
(舍去);
②当点Q在边DC的延长线上(如图2),由PC=CQ得:![]() -x=
-x=![]() x-1,
x-1,
解得x=1.
③当点Q与C点重合,△PCQ不存在.
综上所述,x=0或1时,△PCQ为等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】任意放置以下几何体:正方体、圆柱、圆锥、球体,则三视图都完全相同的几何体是_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】倒数等于它本身的数是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】移动互联网已全面进入人们的日常生活,某市4G用户总数达到3820000,数据3820000用科学记数法表示为( )
A. 3.8×106 B. 3.82×105 C. 3.82×106 D. 3.82×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=-
 x2-
x2- x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;(3)若直线l过点E(4, 0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;(3)若直线l过点E(4, 0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.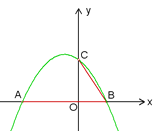
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某地区高度每增加1千米,气温大约降低1.2℃,该地区有一座高3.5千米的山峰,在山脚下测得的温度是15℃,求山顶的温度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断正确的是 ( )
A. 132.4万是精确到十分位得到的 B. 2.40万是精确到千位得到的
C. 2.3×107 是精确到百万位得到的 D. 1.52×106是精确到百分位得到的
相关试题

