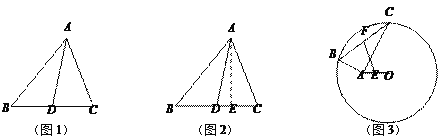
【题目】阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理——“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2.
小明尝试对它进行证明,部分过程如下:
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=……
(1)请你完成小明剩余的证明过程;
理解运用:
(2) ① 在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=_______;
② 如图3,⊙O的半径为6,点A在圆内,且OA=2![]() ,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
拓展延伸:
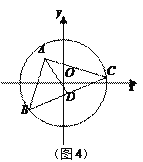
(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5![]() ,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
参考答案:
【答案】(1)证明见解析;(2)①![]() ;②4;(3)10
;②4;(3)10
【解析】试题分析:(1)![]()
=![]()
(2)根据中线长定理即可求解;
(3)根据中线长定理即可求解.
试题解析:(1)∴![]()
=![]()
(2)①![]() ;②4;
;②4;
(3)由(2)的②可知:DE= ![]() ,
,
在△ADE中,AE=![]() , DE=
, DE=![]() ,
,
∴AD长的最大值为![]() +
+![]() =10.
=10.
-
科目: 来源: 题型:
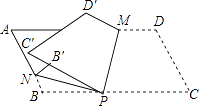
查看答案和解析>>【题目】如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=75°,则∠NPB′=°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果(x+1)(2x+m)的乘积中不含x的一次项,则m的值为( )
A. 2 B. -2 C. 0.5 D. -0.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上出了一道解方程的题
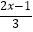 =1﹣
=1﹣ 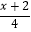 ,小明马上举起了手,要求到黑板上去做,他是这样做的:
,小明马上举起了手,要求到黑板上去做,他是这样做的:
4(2x﹣1)=1﹣3(x+2)①
8x﹣4=1﹣3x﹣6 ②
8x+3x=1﹣6+4 ③
11x=﹣1 ④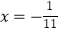 ⑤
⑤
老师说:小明解一元一次方程的一般步骤都掌握了,但解题时有一步做错了,请你指出他错在第步(填编号),错误的原因是;然后,你自己细心地解下列方程: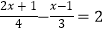 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c满足:①
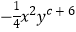 与2x2+ay3的和是单项式; ②
与2x2+ay3的和是单项式; ② 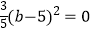 ,
,
(1)求a、b、c的值;
(2)求代数式(5b2﹣3c2)﹣3(b2﹣c2)﹣(﹣c2)+2016abc的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】魔术师为大家表演魔术.他请观众想一个数,然后将这个数按以下步骤操作:

魔术师立刻说出观众想的那个数.
(1)如果小明想的数是﹣1,那么他告诉魔术师的结果应该是;
(2)如果小聪想了一个数并告诉魔术师结果为93,那么魔术师立刻说出小聪想的那个数是;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,请你说出其中的奥妙. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,计算结果错误的是( )
A. (x+2)(x-3)=x2-x-6
B. (x-4)(x+4)=x2-16
C. (2x+3)(2x-6)=2x2-3x-18
D. (2x-1)(2x+2)=4x2+2x-2
相关试题

