【题目】我镇绿色和特色农产品在市场上颇具竞争力.外贸商胡经理按市场价格10元/千克在我区收购了6000千克蘑菇存放入冷库中.请根据胡经理提供的预测信息(如图)帮胡经理解决以下问题:

(1)若胡经理想将这批蘑菇存放x天后一次性出售, 则x天后这批蘑菇的销售单价为 元, 这批蘑菇的销售量是 千克;
(2)胡经理将这批蘑菇存放多少天后,一次性出售所得的销售总金额为100000元;(销售总金额=销售单价×销售量).
(3)将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?
参考答案:
【答案】(1)(10+0.1x); (6000-10x)(2)100;(3)存放110天后出售这批香菇可获得最大利润16500元.
【解析】
试题分析:(1)根据等量关系蘑菇的市场价格每天每千克上涨0.1元则可求出则x天后这批蘑菇的销售单价,再根据平均每天有10千克的蘑菇损坏则可求出这批蘑菇的销售量;
(2)按照等量关系“利润=销售总金额-收购成本-各种费用”列出方程求解即可;
(3)根据等量关系“利润=销售总金额-收购成本-各种费用”列出函数关系式并求最大值.
试题解析:(1)因为蘑菇的市场价格每天每千克上涨0.1元,所以x天后这批蘑菇的销售单价为(10+0.1x)元;
因为均每天有10千克的蘑菇损坏,所以x天后这批蘑菇的销售量是(6000-10x)千克;
(2)由题意得:(10+0.1x)(6000-10x)=100000,
整理得:x2-500x+40000=0,
解方程得:x1=100,x2=400(不合题意,舍去)
所以胡经理将这批蘑菇存放100天后,一次性出售所得的销售总金额为100000元;
(3)设利润为w,由题意得
w=(10+0.1x)(6000-10x)-240x-6000×10,
=-x2+260x=-(x-130)2+16900,
∵a=-1<0,
∴抛物线开口方向向下,
∴x=110时,w最大=16500,
∴存放110天后出售这批香菇可获得最大利润16500元.
-
科目: 来源: 题型:
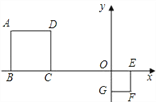
查看答案和解析>>【题目】正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),则这两个正方形的位似中心的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)指定路灯的位置(用点P表示);
(2)在图中画出表示大树高的线段(用线段MG表示);
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.
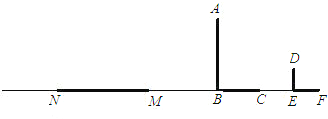
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程kx2﹣6x+9=0有两个不相等的实数根,则k的取值范围( )
A.k<1且k≠0
B.k≠0
C.k<1
D.k>1 -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形ABC中,∠A=40°,则∠B=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果只用正三角形作平面镶嵌(要求镶嵌的正三角形的边与另一正三角形有边重合),则在它的每一个顶点周围的正三角形的个数为( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)的形式来表示(f可用其它字母,但不同的字母表示不同的多项式),例如f(x)=x2+3x﹣5,把x=某数时的多项式的值用f(某数)来表示.
例如x=﹣1时多项式x2+3x﹣5的值记为f(﹣1)=(﹣1)2+3×(﹣1)﹣5=﹣7,
已知g(x)=﹣2x2﹣3x+1,h(x)=ax3+2x2﹣x
(1)求g(﹣2)的值;
(2)若h(﹣2)=14,求g(a)的值.
相关试题

