【题目】如图,在平面直角坐标系中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象分别交于
的图象分别交于![]() ,
,![]() 两点,已知点
两点,已知点![]() 与点
与点![]() 关于坐标原点
关于坐标原点![]() 成中心对称,且点
成中心对称,且点![]() 的坐标为
的坐标为![]() .其中
.其中![]() .
.
(1)四边形![]() 是 .(填写四边形
是 .(填写四边形![]() 的形状)
的形状)
(2)当点![]() 的坐标为
的坐标为![]() 时,且四边形
时,且四边形![]() 是矩形,求
是矩形,求![]() ,
,![]() 的值.
的值.
(3)试探究:随着![]() 与
与![]() 的变化,四边形
的变化,四边形![]() 能不能成为菱形?若能,请直接写出
能不能成为菱形?若能,请直接写出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.

参考答案:
【答案】(1) 平行四边形;(2)![]() ;(3) 四边形
;(3) 四边形 ![]() 不可能成为菱形,理由见解析.
不可能成为菱形,理由见解析.
【解析】(1)根据正、反比例函数的对称性即可得出点A、C关于原点O成中心对称,再结合点B与点D关于坐标原点O成中心对称,即可得出对角线BD、AC互相平分,由此即可证出四边形ABCD的是平行四边形;
(2)由点A的纵坐标结合反比例函数图象上点的坐标特征即可求出n值,进而得出点A的坐标以及OA的长度,再根据矩形的性质即可得出OB=OA,由点B的坐标即可求出m值;
(3)由点A在第一象限内,点B在x轴正半轴上,可得出∠AOB<90°,而菱形的对角线互相垂直平分,由此即可得知四边形ABCD不可能成为菱形.
(1)∵正比例函数y=kx(k>0)与反比例函数y=![]() 的图象分别交于A、C两点,
的图象分别交于A、C两点,
∴点A、C关于原点O成中心对称,
∵点B与点D关于坐标原点O成中心对称,
∴对角线BD、AC互相平分,
∴四边形ABCD的是平行四边形.
故答案为:平行四边形.
(2)∵点A(n,3)在反比例函数y=![]() 的图象上,
的图象上,
∴3n=3,解得:n=1,
∴点A(1,3),
∴OA=![]() .
.
∵四边形ABCD为矩形,
∴OA=![]() AC,OB=
AC,OB=![]() BD,AC=BD,
BD,AC=BD,
∴OB=OA=![]() ,
,
∴m=![]() .
.
(3)四边形ABCD不可能成为菱形,理由如下:
∵点A在第一象限内,点B在x轴正半轴上,
∴∠AOB<90°,
∴AC与BD不可能互相垂直,
∴四边形ABCD不可能成为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市团委举行以“我的中国梦”为主题的知识竞赛,甲、乙两所学校的参赛人数相等,比赛结束后,发现学生成绩分别为
 分,
分,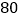 分,
分,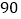 分,
分,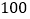 分,并根据统计数据绘制了如下不完整的统计图表:
分,并根据统计数据绘制了如下不完整的统计图表: 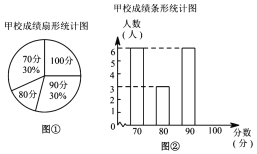
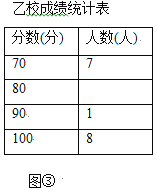
(1)乙学校的参赛人数是 人;
(2)在图①中,“
 分”所在扇形的圆心角度数为 ;
分”所在扇形的圆心角度数为 ;(3)请你将图②补充完整;
(4)求乙校成绩的平均分;
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲列车速度是60km/h,乙列车速度是90km/h.
(1)两列车都从某地出发,目的地距离出发点1000km,甲列车先走2小时,问乙列车什么时候能追上甲列车?追上时离目的地还有多远?
(2)甲列车从A地开往B地,乙列车同时从B地开往A地,已知A,B两地相距200km,两车相遇的地方离A地多远?(用方程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形
 的顶点
的顶点 与坐标原点重合,点
与坐标原点重合,点 的坐标为
的坐标为 ,点
,点 在
在 轴的负半轴上,点
轴的负半轴上,点 ,
, 分别在边
分别在边 ,
, 上,且
上,且 ,
, ,一次函数
,一次函数 的图象过点
的图象过点 和
和 ,反比例函数
,反比例函数 的图象经过点
的图象经过点 ,且与
,且与 的交点为
的交点为 .
.(1)直接写出反比例函数解析式 一次函数的解析式 ;
(2)若点
 在直线
在直线 上,且使△OPM的面积与四边形
上,且使△OPM的面积与四边形 的面积相等,求点
的面积相等,求点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2 , 若y1≠y2 , 取y1、y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 下列判断: ①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x=1.
其中正确的有( )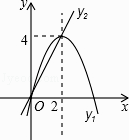
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为4的等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为(结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,BE平分∠ABC,交AD于点E,AB=3cm,ED=
 cm,则平行四边形ABCD的周长是_________.
cm,则平行四边形ABCD的周长是_________.
相关试题

