【题目】二次函数的图象如图所示，以下结论：①；②顶点坐标为；③；④；⑤.正确的有_______.（填序号）

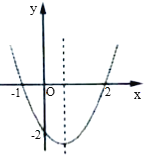
【答案】①⑤

【解析】

根据图象的开口方向可知a>0，根据抛物线与x轴的交点可得对称轴方程，根据抛物线与y轴的交点可得c<0，根据对称轴方程即可确定b的符号，即可对①②③进行判断，根据二次函数的增减性即可对④进行判断，根据点（-1，0）是图象与x轴的交点可对⑤进行判断，综上即可得答案.

∵图象的开口向上，

∴a>0，

∵图象与x轴的交点为（-1，0）和（2，0），

∴对称轴方程为x===>0，

∴b<0，

∵图象与y轴交于y轴负半轴，

∴c<0，

∴abc>0，故①正确，

∵对称轴为x=，图象与y轴交于（0，-2），

∴抛物线顶点坐标不是（，-2），故②错误，

∵=，

∴a+b=0，故③错误，

当x=1时，a+b+c<0，故④错误，

当x=-1时，a-b+c=0，故⑤正确，

综上所述：正确的结论有①⑤，

故答案为：①⑤

关闭