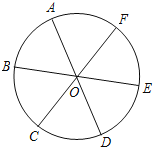
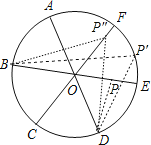
【题目】如图,点A、B、C、D、E、F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )
A.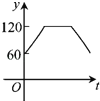 B.
B.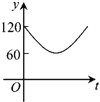 C.
C.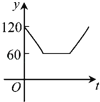 D.
D.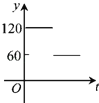
参考答案:
【答案】C
【解析】
试题分析:利用点A、B、C、D、E、F为⊙O的六等分点可得到∠BOC=∠COD=60°,所以P在O点时,∠BPD=120°,P在弧EF上时,∠BPD=![]() ∠BOD=60°,然后分类讨论:当点P从O点运动到E点时,易得y由120°逐渐减小到60°;当点P在弧EF上运动时,y=60°;当点P从F点运动到O点时,易得y由60°逐渐增大到120°,根据此特征可对四个选项进行判断.
∠BOD=60°,然后分类讨论:当点P从O点运动到E点时,易得y由120°逐渐减小到60°;当点P在弧EF上运动时,y=60°;当点P从F点运动到O点时,易得y由60°逐渐增大到120°,根据此特征可对四个选项进行判断.
解:因为点A、B、C、D、E、F为⊙O的六等分点,
所以∠BOC=∠COD=60°,
当P在O点时,∠BPD=120°,当P在弧EF上时,∠BPD=![]() ∠BOD=60°,
∠BOD=60°,
当点P从O点运动到E点时,y由120°逐渐减小到60°;当点P在弧EF上运动时,y的值不变,为60°;当点P从F点运动到O点时,y由60°逐渐增大到120°.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(a+b)2=25,(a﹣b)2=9,求ab与a2+b2的值.
-
科目: 来源: 题型:
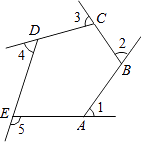
查看答案和解析>>【题目】如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5= .
-
科目: 来源: 题型:
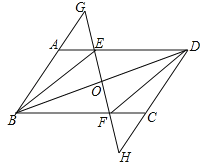
查看答案和解析>>【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点0.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什幺特殊四边形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E是AD上的一点,且AE=
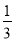 AD,对角线AC,BD交于点O,EC交BD于F,BE交AC于G,如果平行四边形ABCD的面积为S,那么,△GEF的面积为( )
AD,对角线AC,BD交于点O,EC交BD于F,BE交AC于G,如果平行四边形ABCD的面积为S,那么,△GEF的面积为( )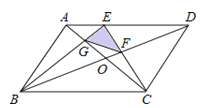
A.
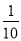 S B.
S B. 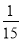 S C.
S C. 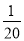 S D.
S D. 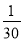 S
S -
科目: 来源: 题型:
查看答案和解析>>【题目】将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
A.h≤17
B.h≥8
C.15≤h≤16
D.7≤h≤16 -
科目: 来源: 题型:
查看答案和解析>>【题目】命题“两直线平行,同位角相等”的逆命题是________________________
相关试题

