【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。
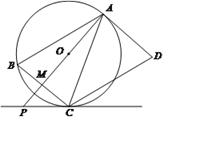
(1) 判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
参考答案:
【答案】(1)相切;证明见解析;(2)![]() .
.
【解析】试题分析:(1)通过分析,直线与圆O已经有一个公共点,连接半径0C,只要证明OC⊥PC即可;(2)根据AD是切线和AD∥BC证明AP⊥BC,利用垂径定理计算出CM=BM=3,在Rt△AMB中,利用勾股定义计算出AM的长,在Rt△OMC中,利用勾股定理建立方程计算出圆O的半径的长,最后证明△OMC~△OCP,利用相似三角形的对应边成比例计算出PC的长.
试题解析:(1) 直线PC与圆O相切.
连接CO并延长,交圆O于点N,连接BN.
∵AB//CD,
∴BAC=ACD.
∵BAC=BNC,
∴BNC=ACD.
∵BCP=ACD,
∴BNC=BCP.
∵CN是圆O的直径,
∴CBN=90°.
∴BNC+BCN=90°,
∴BCP+BCN=90°.
∴PCO=90°,即PC^OC.
又∵点C在圆O上,
∴直线PC与圆O相切.
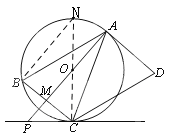
(2) ∵AD是圆O的切线,
∴AD^OA,即OAD=90°.
∵BC//AD,
∴OMC=180°-OAD=90°,即OM^BC.
∴MC=MB.
∴AB=AC.
在Rt△AMC中,AMC=90°,AC=AB=9,MC=![]() BC=3,
BC=3,
由勾股定理,得AM=![]() =
=![]() =6
=6![]() .
.
设圆O的半径为r.
在Rt△OMC中,OMC=90°,OM=AM-AO=6![]() -r,MC=3,OC=r,
-r,MC=3,OC=r,
由勾股定理,得OM 2+MC 2=OC 2,
∴(6![]() -r)2+32=r2.
-r)2+32=r2.
解得r=![]() .
.
在△OMC和△OCP中,
∵OMC=OCP,MOC=COP,
∴△OMC~△OCP.
∴![]() =
=![]() ,即
,即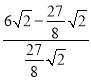 =
=![]() .
.
∴PC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,属于必然事件的是( )
A.2020年的除夕是晴天B.太阳从东边升起
C.打开电视正在播放新闻联播D.在一个都是白球的盒子里,摸到红球
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图7,△ABC是等腰直角三角形,AC=BC=
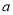 ,以斜边AB上的点O为圆心的圆分别与AC,BC相切与点E,F, 与AB 分别交于点G,H,且 EH 的延长线和 CB 的延长线交于点D,则 CD 的长为 .
,以斜边AB上的点O为圆心的圆分别与AC,BC相切与点E,F, 与AB 分别交于点G,H,且 EH 的延长线和 CB 的延长线交于点D,则 CD 的长为 .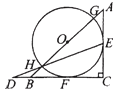
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的外接圆圆心是该三角形( )的交点.
A.三条边垂直平分线B.三条中线
C.三条角平分线D.三条高
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,∠B+∠D=260°,那么∠A的度数是( )
A. 130° B. 100° C. 50° D. 80°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
考试类别
平时
期中考试
期末考试
第一单元
第二单元
第三单元
第四单元
成绩
88
86
90
92
90
96

(1)李刚同学6次成绩众数是 .
(2)李刚同学6次成绩的中位数是 .
(3)李刚同学平时成绩的平均数是 .
(4)如果用下图的权重给李刚打分,他应该得多少分?(满分100分,写出解题过程) -
科目: 来源: 题型:
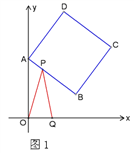
查看答案和解析>>【题目】如图1,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标
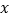 (长度单位)关于运动时间t(秒)的函数图象如图2所示,请写出点Q开始运动时的坐标及点P运动速度;
(长度单位)关于运动时间t(秒)的函数图象如图2所示,请写出点Q开始运动时的坐标及点P运动速度;(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.
(4)如果点P、Q保持原速度速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.
相关试题

