Question

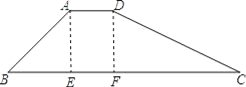
【题目】如图，在梯形ABCD中，AD∥BC，∠B=45°，AD=8，AB=，CD=26，求BC的长．

Answer 1

【答案】42.

【解析】作AE⊥BC，DF⊥BC，垂足分别为E、F，由此可得出四边形AEFD是矩形，在Rt△ABE中利用勾股定理可求出AE的长，在Rt△DFC中利用勾股定理可求出FC的长，再根据线段之间的关系即可得出BC的长．

解：作AE⊥BC，DF⊥BC，垂足分别为E、F，如图所示．

∵AE⊥BC，DF⊥BC，

∴∠AEF=∠DFE=90°，AE∥DF．

∵AD∥BC，

∴四边形AEFD是矩形，

∴AE=DF，AD=EF=8．

在Rt△ABE中，由∠B=45°，得AE=BE

∴，

∴AE=BE=10，

∴DF=10．

在Rt△DFC中，由DF=10，CD=26，

∴FC==24，

∴BC=BE+EF+FC=42．

“点睛”本题考查了条形的性质即直角三角形的性质，属于基础题，关键将作为的知识结合，做题时融会贯通.