【题目】在Rt△ABC中，，AC=3，BC=4．点O为边AB上一点（不与A重合）⊙O是以点O为圆心，AO为半径的圆．当⊙O与三角形边的交点个数为3时，则OA的范围（ ）

A.或B.或

C.D.或

【答案】B

【解析】

根据题意可以画出相应的图形，然后即可得到OA的取值范围，本题得以解决．

如图所示，


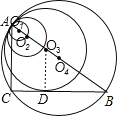
当圆心从O1到O3的过程中，⊙O与三角形边的交点个数为3，当恰好到达O3时则变为4个交点，
作O3D⊥BC于点D，
则∠O3BD=∠ABC，
∵在Rt△ABC中，∠ACB=90°，AC=3，BC=4，
∴AB=5，
设O3A=a，则O3B=5-a，
∴ ，得a=，
∴当0＜OA＜时，⊙O与三角形边的交点个数为3，
当点O为AB的中点时，⊙O与三角形边的交点个数为3，此时OA=2.5，
由上可得，0＜OA＜或OA=2.5时，⊙O与三角形边的交点个数为3，
故选：B．

关闭