【题目】已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A.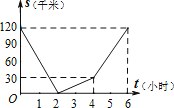
B.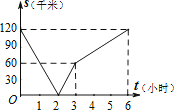
C.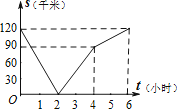
D.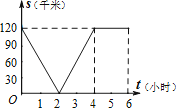
参考答案:
【答案】B
【解析】解:根据题意,两人同时相向出发,甲到达B地时间为:![]() =6小时,乙到达A地:
=6小时,乙到达A地:![]() =3小时.
=3小时.
根据题意,分成两个阶段:相遇前、相遇后;相遇后可分成乙到达A地、甲到达B地;
相遇前,s=120﹣(20+40)t=120﹣60t(0≤t≤2),当两者相遇时,t=2,s=0,
相遇后,当乙到达A地前,甲乙均在行驶,即s=(20+40)(t﹣2)=60t﹣120(2≤t≤3),当乙到达A地时,此时两者相距60千米;
当乙到达A地后,剩下甲在行驶,即s=60+20(t﹣3)=20t(3≤t≤6),
故: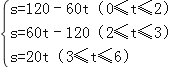
法二:本题可无需列出方程,只需弄清楚题意,分清楚s与t的变化可分为几个阶段:相遇前、相遇后;相遇后可分成乙到达A地、甲到达B地,故求出各个时间点便可.
∵A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A,
∴两人同时出发,2小时两人就会相遇,甲6小时到达B地,乙3小时到达A地,
故两人之间的距离为s(千米),甲行驶的时间为t(小时),则正确反映s与t之间函数关系的是B.
故选:B.
根据题意求出2小时两人就会相遇,甲6小时到达B地,乙3小时到达A地,进而根据相遇前、相遇后两个阶段得出相应的分段函数,从而找出符合题意的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xoy中,抛物线
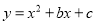 经过点A(0,-3),B(4,5).
经过点A(0,-3),B(4,5).(1)求此抛物线表达式及顶点M的坐标;
(2)设点M关于y轴的对称点是N,此抛物线在A,B两点之间的部分记为图象W(包含A,B两点),经过点N的直线l:
 与图象W恰一个有公共点,结合图象,求m的取值范围.
与图象W恰一个有公共点,结合图象,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列一元二次方程中,有两个不相等实数根的是( )
A.x2=-x
B.x2+4x+4=0
C.x2+2=2x
D.(x-1) 2+2=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
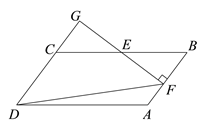
(1)求证:GD=GF.
(2)已知BC=10,
 .求 CD的长.
.求 CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AD是角平分线,若∠B=50,∠C=70 ,则∠ADC=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
A.平均数
B.中位数
C.众数
D.方差 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于抛物线y=(x+1) 2+2的说法,正确的是( )
A.开口向下
B.对称轴是直线x=1
C.当x=-1时,y有最小值2
D.当x>-1时,y随x的增大而减小
相关试题

