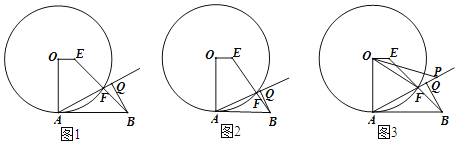
【题目】如图，OA是⊙O的半径，点E为圆内一点，且OA⊥OE，AB是⊙O的切线，EB交⊙O于点F，BQ⊥AF于点Q．

(1)如图1，求证：OE∥AB；

(2)如图2，若AB＝AO，求的值；

(3)如图3，连接OF，∠EOF的平分线交射线AF于点P，若OA＝2，cos∠PAB＝，求OP的长．

【答案】(1)证明见解析；(2)；(3)．

【解析】

（1）利用切线的性质证得∠AOE+∠OAB=180°，利用同旁内角互补两直线平行证得OE∥AB；
（2）过O点作OC⊥AF于点C，证得△AOC≌△BAQ（AAS）后得到AC=BQ，进一步得到AF=2AC=2BQ，从而求得两条线段的比；
（3）过O点作OC⊥AF于点C，解直角三角形求得OC的长，然后证得△POC为等腰直角三角形，利用等腰三角形的性质求得线段OP 的长即可．

解：(1)

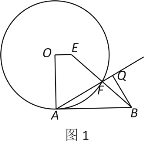∵OA⊥OE，

∴∠AOE=90°，

又∵AB是⊙O的切线，OA是⊙O的半径，

∴OA⊥AB

∴∠OAB=90°，

∴∠AOE+∠OAB =180°，

∴OE∥AB.

(2)如图2，过O点作OC⊥AF于点C，

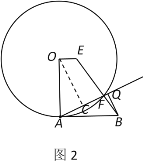
∴AF=2AC， ∠OCA=90°，

∴∠AOC+∠OAC =90°，

又∵OA⊥AB，

∴∠OAC+∠CAB =90°，

∴∠AOC=∠CAB，

又∵BQ⊥AF，

∴∠AQB =90°，

∴∠ACO =∠AQB

又∵OA =AB，

∴△AOC≌△BAQ(AAS)，

∴AC =BQ，

∴AF=2AC =2BQ，

即；

(3)如图3：过O点作OC⊥AF于点C，

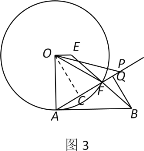
由(2)得∠AOC =∠PAB，

∴，

在Rt△AOC中， OA =2，

∴OC===，

又∵OA=OF，OC⊥AF于点C，

∴∠COF=∠AOF，

又∵OP平分∠EOF，

∴∠POF=∠EOF，

∴∠POC=∠COF+∠POF=∠AOF+∠EOF=∠EOA=45°，

∴△POC为等腰直角三角形

∴．

关闭